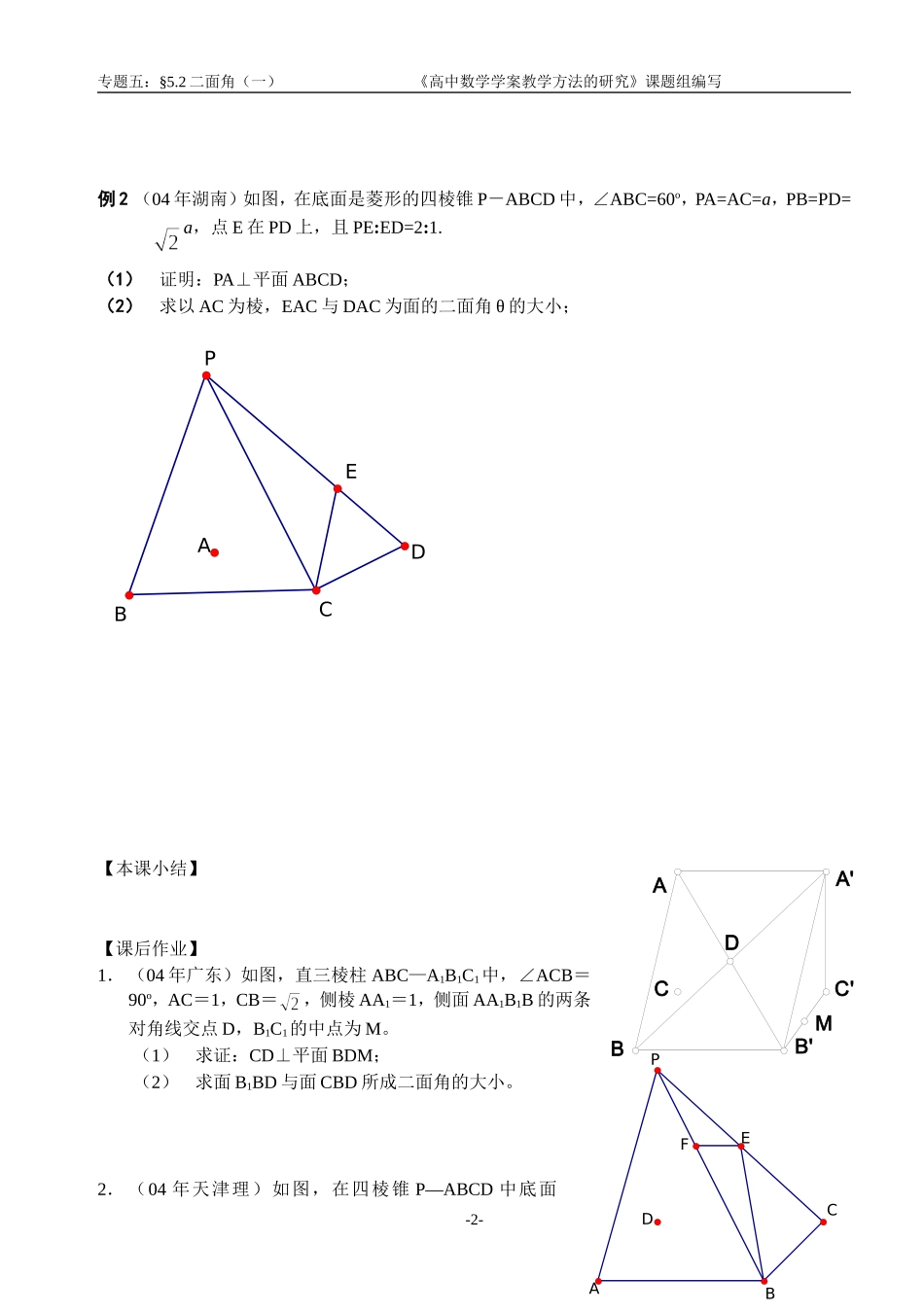
§5.2二面角(一)【高考热点】1.二面角的问题是高考立体几何部分必考的内容,也是立体几何的一大难点;2.二面角的平面角的作法:(一)定义法;(二)垂面法;(三)三垂线定理法(主要方法);3.二面角的平面角的计算方法:(1)作出角再计算;(2)利用公式(此法有争议).【课前预习】1.在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成角的大小等于.(结果用反三角函数值表示)2.(04年重庆)设P是的二面角内一点,AB为垂足,则AB的长为()A.B.C.D.3.在边长为1的菱形ABCD中,∠ABC=60°,将菱形沿对角线AC折起,使折起后BD=1,则二面角B-AC-D的余弦值为.4.(04湖北理)已知平面所成的二面角为80°,P为、外一定点,过点P的一条直线与、所成的角都是30°,则这样的直线有且仅有()A.1条B.2条C.3条D.4条【典型例题】例1(04年浙江)如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=,AF=1,M是线段EF的中点。(1)求证:AM∥平面BDE;(2)求证:AM⊥平面BDF;(3)求二面角A-DF-B的大小.MCDABEF专题五:§5.2二面角(一)《高中数学学案教学方法的研究》课题组编写例2(04年湖南)如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60o,PA=AC=a,PB=PD=a,点E在PD上,且PE:ED=2:1.(1)证明:PA⊥平面ABCD;(2)求以AC为棱,EAC与DAC为面的二面角θ的大小;【本课小结】【课后作业】1.(04年广东)如图,直三棱柱ABC—A1B1C1中,∠ACB=90o,AC=1,CB=,侧棱AA1=1,侧面AA1B1B的两条对角线交点D,B1C1的中点为M。(1)求证:CD⊥平面BDM;(2)求面B1BD与面CBD所成二面角的大小。2.(04年天津理)如图,在四棱锥P—ABCD中底面--2ABDCPEABCA'B'C'DMEBDCAPFABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,作EF⊥PB于点F.(1)证明PA∥平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C-PB-D的大小.