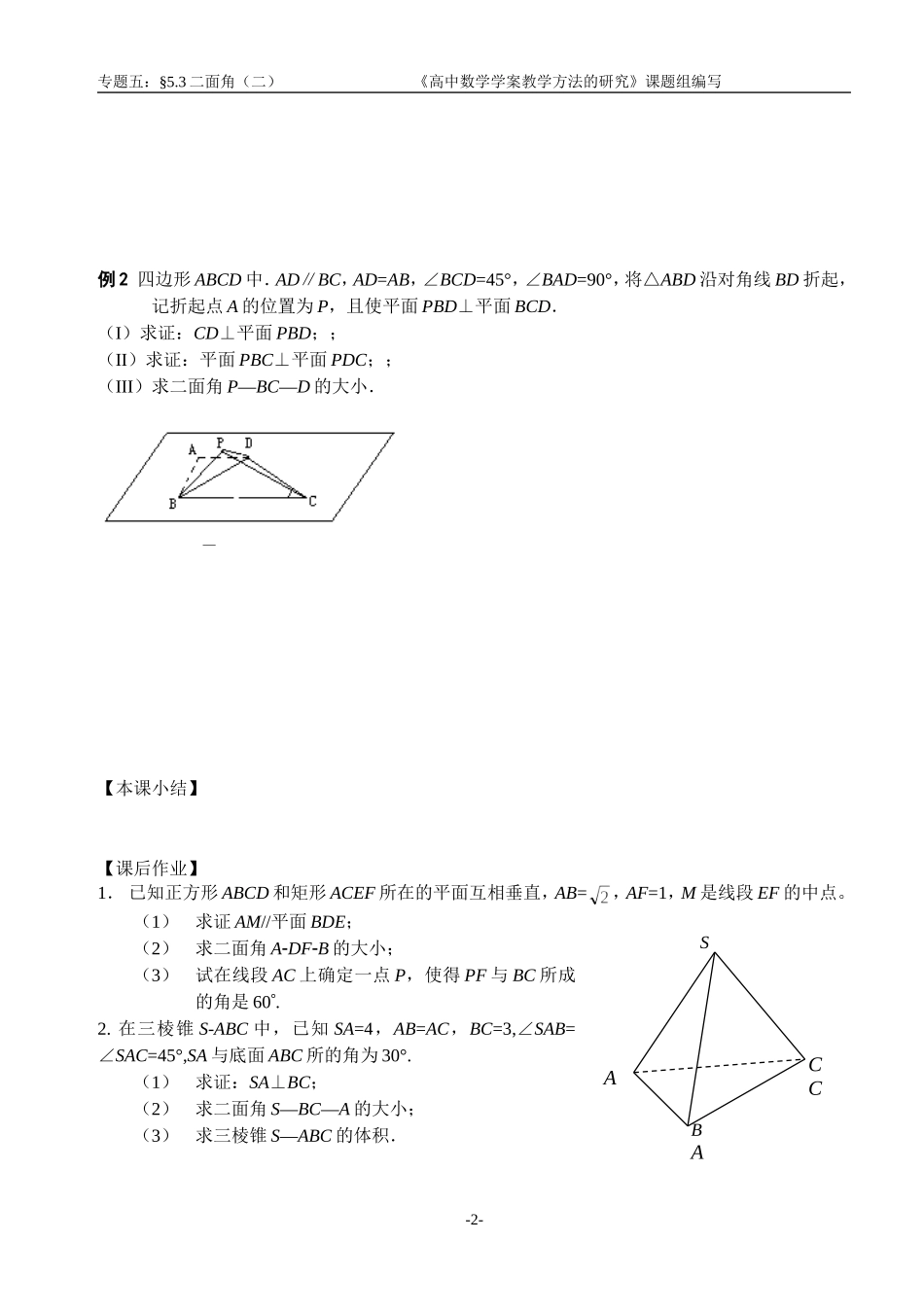
§5.2二面角(二)【高考热点】1.以多面体和旋转体为载体的线面位置关系的论证以及二面角的探求是高考中考查学生立体几何掌握情况的主要方法,其中尤以正方体,三(四)棱锥,三棱柱为载体居多;2.二面角的探求最能体现空间问题平面化的化规思想,是立体几何的精髓也是高考考查的重点.【课前预习】1.在边长为a的正三角形ABC中,AD垂直BC于D,沿AD折成二面角B-AD-C后,BC=,这时二面角B-AD-C的大小为()A.B.C.D.2.直三棱柱ABC-A1B1C1中∠ABC=900,AB=4,BC=AA1=2,求:(1)求B1C与A1B所成的角;(2)求面AB1C和A1B所成角;(3)求二面角B-AC-B1的大小.【典型例题】例1如图,四棱锥中,底面,.底面为直角梯形,∥,,.点在棱上,且.(Ⅰ)求异面直线与所成的角;(Ⅱ)求证:∥平面;(Ⅲ)求二面角的大小.PADBCE专题五:§5.3二面角(二)《高中数学学案教学方法的研究》课题组编写例2四边形ABCD中.AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起,记折起点A的位置为P,且使平面PBD⊥平面BCD.(I)求证:CD⊥平面PBD;;(II)求证:平面PBC⊥平面PDC;;(III)求二面角P—BC—D的大小.【本课小结】【课后作业】1.已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点。(1)求证AM//平面BDE;(2)求二面角A-DF-B的大小;(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°.2.在三棱锥S-ABC中,已知SA=4,AB=AC,BC=3,∠SAB=∠SAC=45°,SA与底面ABC所的角为30°.(1)求证:SA⊥BC;(2)求二面角S—BC—A的大小;(3)求三棱锥S—ABC的体积.--2SCCBAA