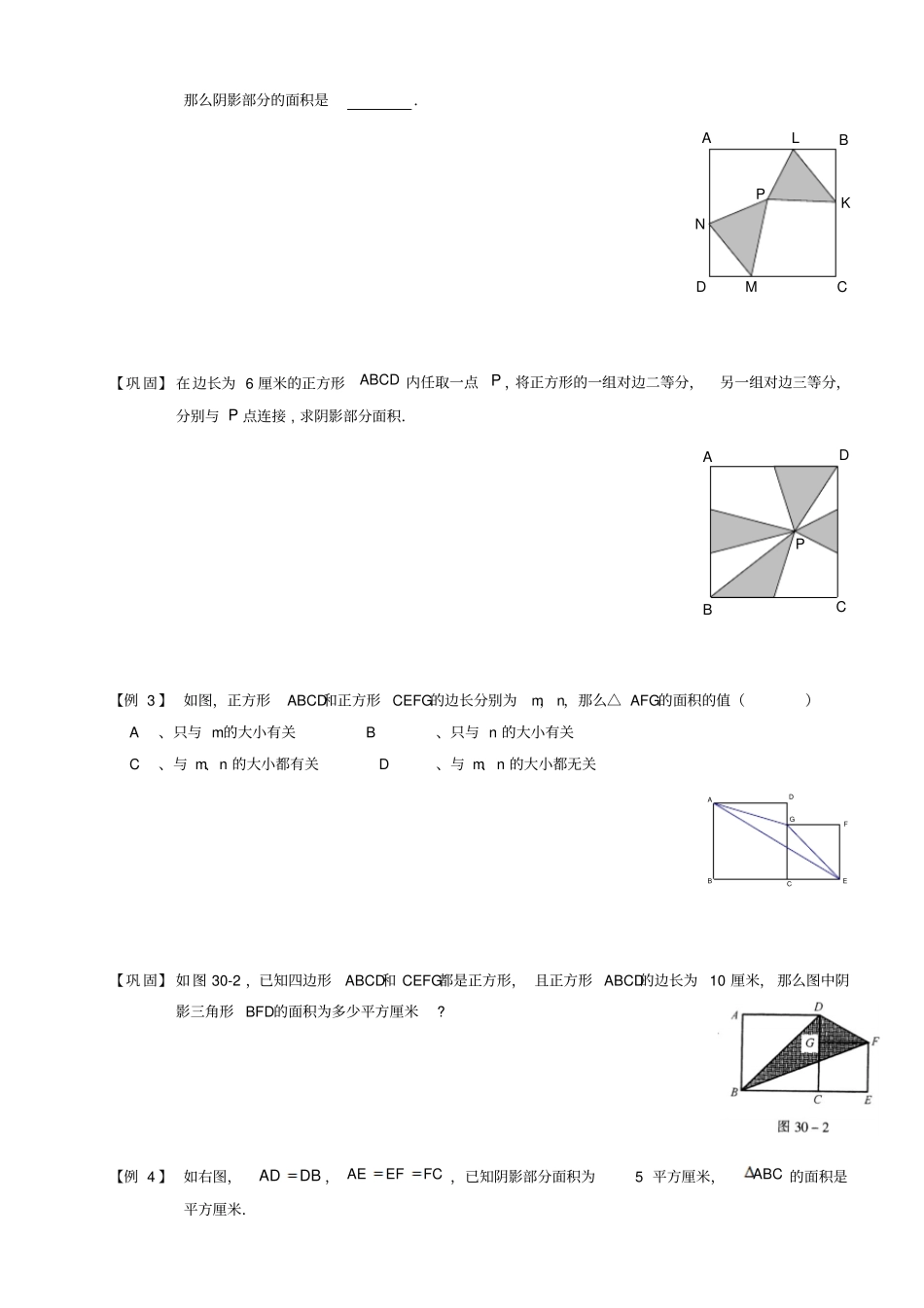
板块一三角形等高模型我们已经知道三角形面积的计算公式:三角形面积底高2从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小);如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论:①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如左图12::SSabbaS2S1DCBA③夹在一组平行线之间的等积变形,如右上图ACDBCDSS△△;反之,如果ACDBCDSS△△,则可知直线AB平行于CD.④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.知识框架三角形等高模型和鸟头模型板块二鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC△中,,DE分别是,ABAC上的点如图⑴(或D在BA的延长线上,E在AC上),则:():()ABCADESSABACADAE△△EDCBADECBA【例1】如右图,E在AD上,AD垂直BC,12AD厘米,3DE厘米.求三角形ABC的面积是三角形EBC面积的几倍?EDCBA【巩固】如图30-5,设正方形ABCD的面积为1,E,F分别为边AB,AD的中点,FC=3GC,则阴影部分的面积是多少?【例2】ABCD是边长为12的正方形,如图所示,P是内部任意一点,4BLDM、5BKDN,例题精讲那么阴影部分的面积是.PNMLKDCBA【巩固】在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.PDCBA【例3】如图,正方形ABCD和正方形CEFG的边长分别为m,n,那么△AFG的面积的值()A、只与m的大小有关B、只与n的大小有关C、与m、n的大小都有关D、与m、n的大小都无关GFEDCBA【巩固】如图30-2,已知四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为10厘米,那么图中阴影三角形BFD的面积为多少平方厘米?【例4】如右图,ADDB,AEEFFC,已知阴影部分面积为5平方厘米,ABC的面积是平方厘米.FEDCBA【巩固】图中三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍.那么三角形AEF的面积是多少平方厘米?FEDCBA【例5】如图所示,四边形ABCD与AEGF都是平行四边形,请你证明它们的面积相等.GFEDCBA【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?ABGCEFD【例6】如图,如果长方形ABCD的面积是56平方厘米,那么四边形MNPQ的面积是多少平方厘米?6523NMQPDCBA【巩固】如图,阴影部分四边形的外接图形是边长为10cm的正方形,则阴影部分四边形的面积是2cm.1cm4cm【例7】如图在ABC△中,,DE分别是,ABAC上的点,且:2:5ADAB,:4:7AEAC,16ADES△平方厘米,求ABC△的面积.EDCBA【巩固】如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?EDCBA【例8】如图在ABC△中,D在BA的延长线上,E在AC上,且:5:2ABAD,:3:2AEEC,12ADES△平方厘米,求ABC△的面积.EDCBA【巩固】如图,三角形ABC的面积为3平方厘米,其中:2:5ABBE,:3:2BCCD,三角形BDE的面积是多少?ACDCEBA【例9】图中三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍.那么三角形AEF的面积是多少平方厘米?FEDCBA【巩固】如图,三角形ABC中,2DCBD,3CEAE,三角形ADE的面积是20平方厘米,三角形ABC的面积是多...