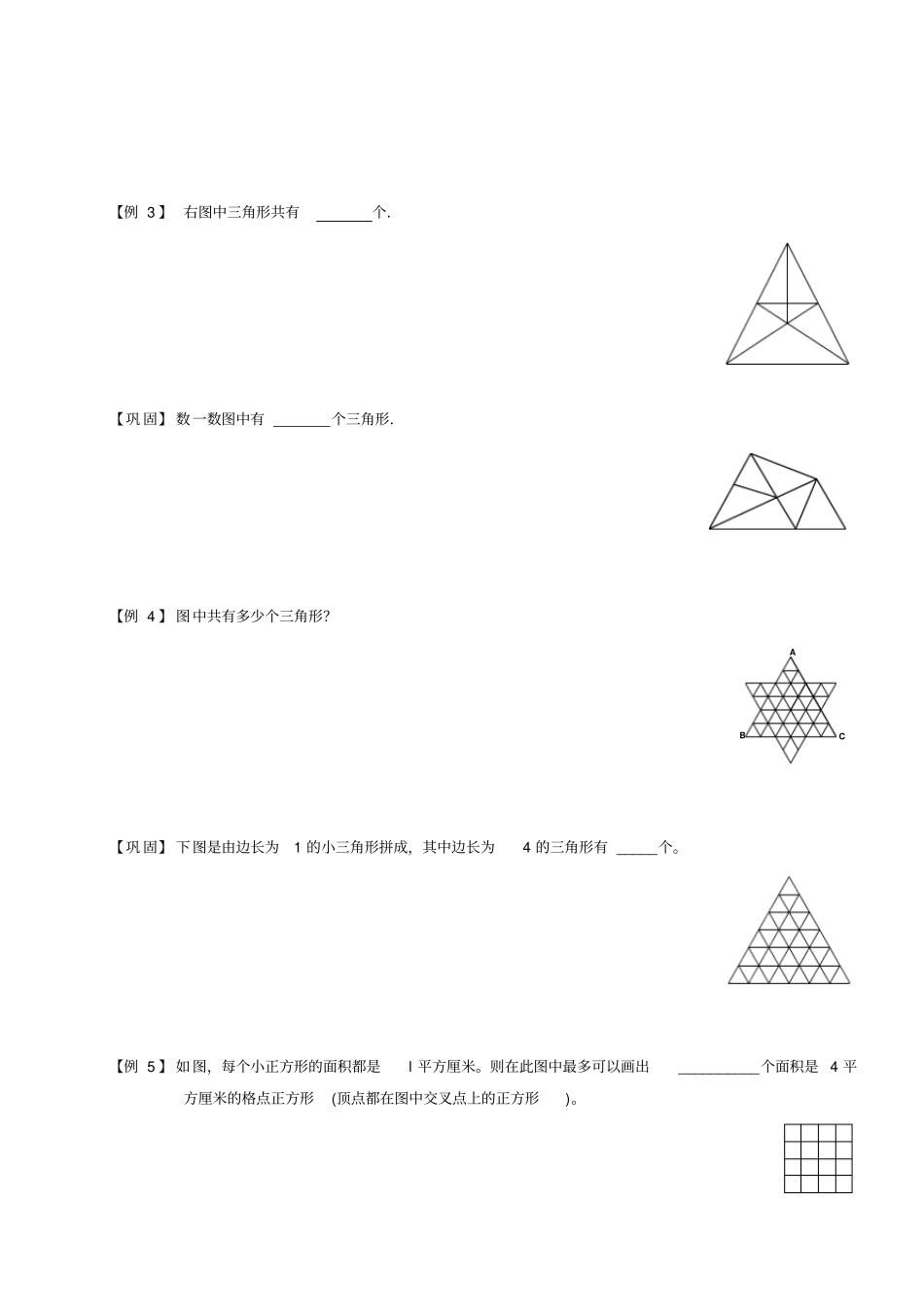
一、公式计算法几何计数内容很广,包括数线段的条数,角的个数,长方形、正方形、三角形、平行四边形、梯形等图形的个数,也包括数立体图形的个数。图形的计数一般有两种思考方法:公式计算法和分类计数法。三年级学习的线段、长方形和正方形的计数就属于公式计算法。(1)一条线段有两个端点,若这条线段上有n个点,那么线段总数是(n-1)+(n+2)+⋯+3+2+1(2)如果一个长方形的长边上有n个小格,宽边上有m个小格,那么长方形的总数是(1+2+3+⋯+n)×(1+2+⋯+m)(3)如果把正方形各边都n等分,那么正方形的总数是n2+(n-1)2+(n-2)2+⋯+32+22+12上面计算线数的方法也可用于计算角的个数,而且,根据这些计数方法在以后还可以类推出立体图形的计算方法。二、对应法将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.(1)分类数图形。(2)对应法数图形。例题精讲重难点知识结构几何计数一、分类数图形【例1】下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的.如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍,那么围成的图形有几层,共用了多少根小棍?【巩固】如图所示,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?【例2】图中有______个正方形.【巩固】数一数:图中共有________个正方形。【例3】右图中三角形共有个.【巩固】数一数图中有_______个三角形.【例4】图中共有多少个三角形?CBA【巩固】下图是由边长为1的小三角形拼成,其中边长为4的三角形有_____个。【例5】如图,每个小正方形的面积都是l平方厘米。则在此图中最多可以画出__________个面积是4平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。【巩固】图中的每个小方格都是面积为1的正方形,面积为2的矩形有个。二、对应法数图形【例6】在8×8的方格棋盘中,取出一个由三个小方格组成的“L”形(如图),一共有多少种不同的方法?【例7】在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个?【巩固】用一张如图所示的纸片盖住66方格表中的四个小方格,共有多少种不同的放置方法?三、几何计数综合【例8】如图,连接一个正六边形的各顶点.问图中共有多少个等腰三角形(包括等边三角形)?【巩固】如右图是一个跳棋棋盘,请你算算棋盘上共有多少个棋孔?【例9】如图所示,在直线AB上有7个点,直线CD上有9个点.以AB上的点为一个端点、CD上的点为另一个端点的所有线段中,任意3条线段都不相交于同一个点,求所有这些线段在AB与CD之间的交点数.CDBA【巩固】图中可数出的三角形的个数为.【例10】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?面积等于2平方厘米的三角形有多少个?【巩固】下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?【例11】一张长方形纸片,长是宽的2倍,先对折成正方形,再对折成长方形,再对折成正方形,⋯⋯,共对折7次,将纸打开展平,数一数用折痕分割成的正方形共有多少个?【巩固】将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作.按上述规则完成五次操作后,剪去所得的小正方形的左下角.问:当展开这张正方形纸后,一共有多少个小洞孔?【例12】一个圆上有12个点A1,A2,A3,⋯,A11,A12.以它们为顶点连三角形,使每个点恰好是一个三角形的顶点,且各个三角形的边都不相交.问共有多少种不同的连法?A12A11A10A9A8A7A6A5A4A3A2A1【随练1】数一数,图中有_________________个三角形。【随练2】用3根等长的火柴可以摆成一个等边三角形.如图用这样的等边三角形拼合成一个...