四边形复习教学反思VIP免费

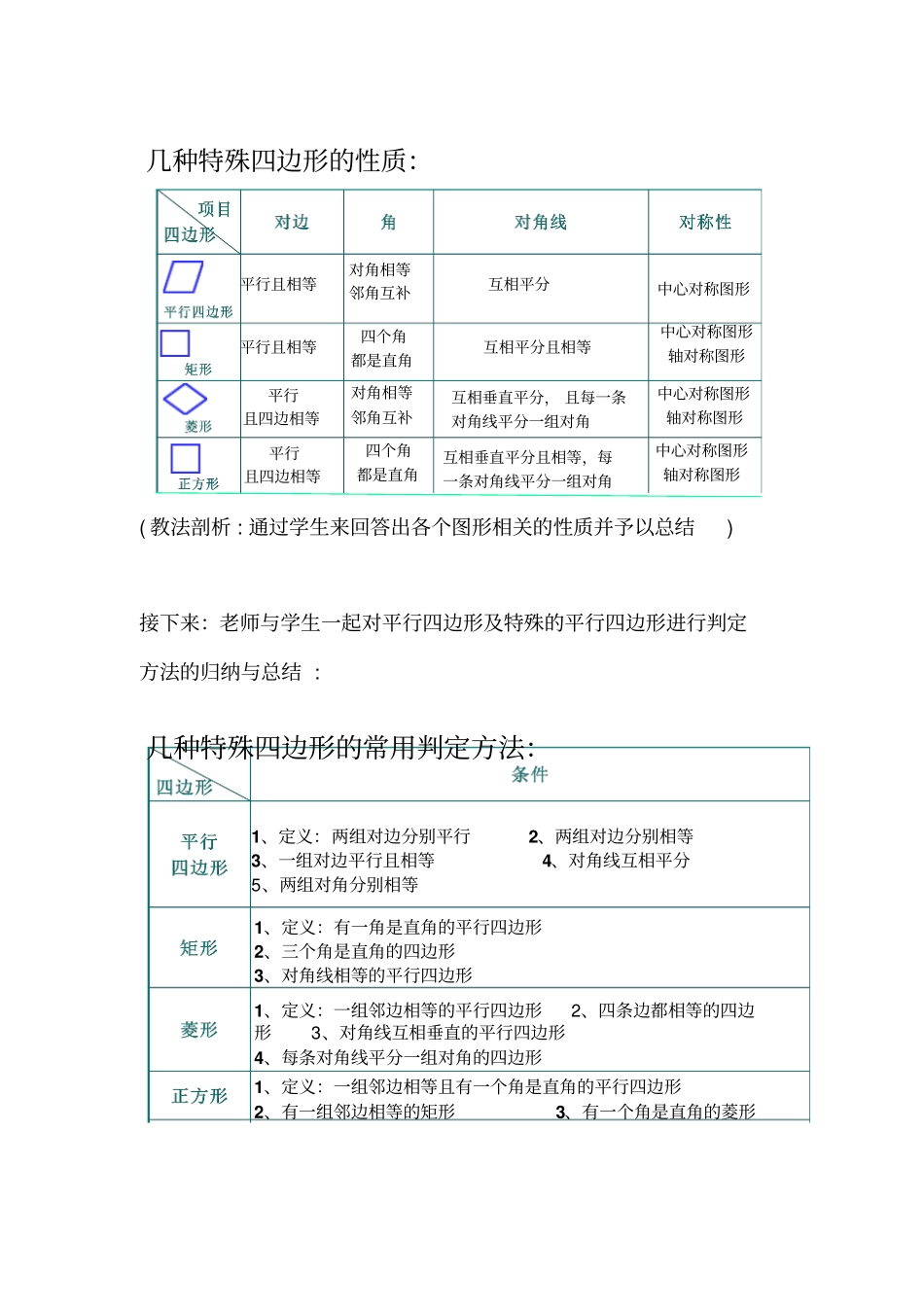
四边形复习教学反思前言：本周主要进行了平行四边形及特殊的平行四边形的复习，从展示学生归纳的特殊的精心设计例题，有意识地创设了引人入胜步步深化的练习，旨在形成激发学生主动参与、积极思维、合作学习解决问题的良好教学氛围。平行四边形的知识结构图入手，回顾了特殊的平行四边形的定义、性质、判定及特殊的平行四边形之间内在的联系及从属关系，接着又总结本次教学比较成功之处一、有关学生4月18日、19日两天我区七年级、八年级正好进行期中考试，上复习课。于是选择这个题材进行教学，共同来研讨复习课的上法。二、有关教材新教材和原来的教材相比有了很大的变化，如新教材中没有梯形这部分内容，课程的编写特点也有一些变化。我在进行教学设计时把这节课的内容进行了细化，并把教材的内容进行了梳理和重组，在教学手段的预设中尽量做到融知识生成与解决途径于活动中。三、有关教学理论、教学模式及教学策略1﹑有关教学理论：用“建构主义学习理论”及“人本主义学习理论”为基础；2﹑教学模式：采用“知识归纳—实践应用”教学模式,在教学手段的预设中尽量做到融知识生成与解决途径于活动中。3﹑教学策略：采用“合作式”教学策略.四、有关教学过程首先，老师与学生一起归纳相关的定义：(教法剖析:用多媒体给出导入,既节约时间又便于学生主动参与学习和开展合作学习,也有利个别化学习和小组合作学习等).接着：老师与学生一起对平行四边形及特殊的平行四边形进行性质的归纳与总结：两组对边分别平行有一个角是直角邻边相等邻边相等有一个角是直角四边形平行四边形矩形菱形正方形有一个角是直角且邻边相等(教法剖析:通过学生来回答出各个图形相关的性质并予以总结)接下来：老师与学生一起对平行四边形及特殊的平行四边形进行判定方法的归纳与总结:几种特殊四边形的常用判定方法：1、定义：两组对边分别平行2、两组对边分别相等3、一组对边平行且相等4、对角线互相平分5、两组对角分别相等1、定义：有一角是直角的平行四边形2、三个角是直角的四边形3、对角线相等的平行四边形1、定义：一组邻边相等的平行四边形2、四条边都相等的四边形3、对角线互相垂直的平行四边形4、每条对角线平分一组对角的四边形1、定义：一组邻边相等且有一个角是直角的平行四边形2、有一组邻边相等的矩形3、有一个角是直角的菱形平行且相等平行且相等平行且四边相等平行且四边相等对角相等邻角互补四个角都是直角对角相等邻角互补四个角都是直角互相平分互相平分且相等互相垂直平分，且每一条对角线平分一组对角互相垂直平分且相等，每一条对角线平分一组对角中心对称图形中心对称图形轴对称图形中心对称图形轴对称图形中心对称图形轴对称图形几种特殊四边形的性质：(教法剖析:通过学生来回答出各个图形相关的判定方法并予以总结)接下来：老师给出了以下一组同步练习:(教法剖析:让全班进入随堂练习状态,并让首先完成的两个小组上去展示,有小组的奖励加分,再次调动学生的学习激情,使学生的注意力高度集中在老师创设的情境中)接下来：老师给出了以下与中考有关的拓展练习:12．已知菱形两条对角线的长分别为10cm和9cm，则这个菱形的面积是______cm2．13、如图，菱形ABCD的对角线AC、BD相交于点O，且AC＝8，BD＝6，过点O作OH丄AB，垂足为H，则点O到边AB的距离是____11.如图，在菱形ABCD中，∠BAD=60°，BD=4，则菱形ABCD的周长是_______．重热点五特殊平行四边形的性质和判定(教法剖析:通过“中考链接”式的学生极关心的拓展练习,把学生的注意力从课内延展到课外,无形中扩大了教学效果的影效应)以构建主义理论为依据，采用“情境――探究”教学模式与合作式教学相结合的教学模式．五、有关课例后的几点思考通过这节案例课，我们组的学员认识到：“探索是教学的生命线”,在平时的数学活动中要摒弃“重结论，轻过程”的传统教学思想，要从学生已有的知识和生活体验出发，让学生经历“问题情境——建立模型——解释应用与拓展”的过程，引导学生积极参与知识的形成过程和探求过程，给学生以充分从事数学活动的时间、空间。⑴教学中要注意基本概念的教学。数学中的概念简洁、抽象，如何让其形象化，使其生...