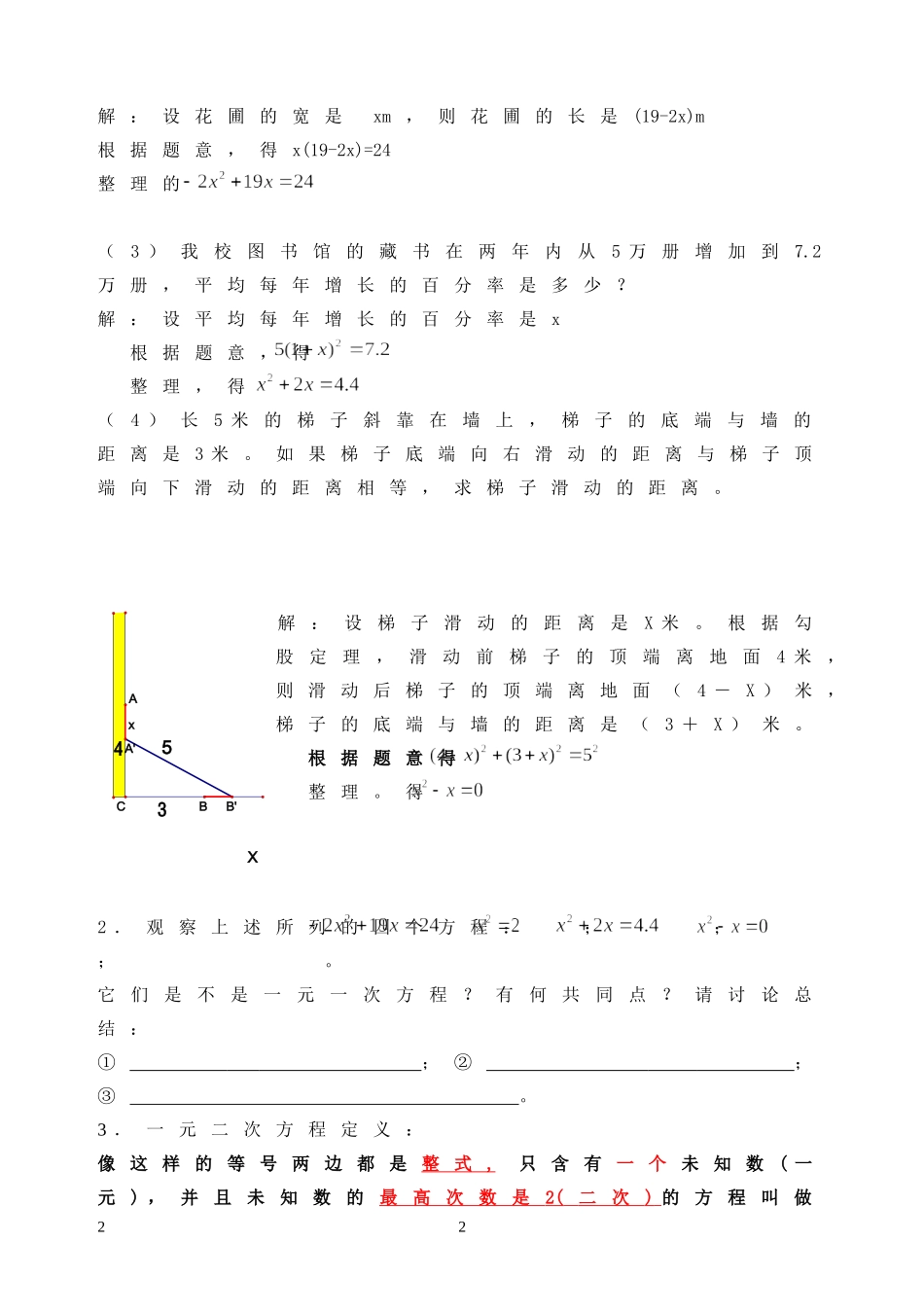
第一章一元二次方程1.1一元二次方程教案学习目标:1.通过观察,归纳一元二次方程的概念。理解掌握一元二次方程的一般形式(≠0)2.在分析、揭示实际问题的数量关系并把实际问题转化为数学模型(一元二次方程)的过程中使学生感受方程是刻画现实世界数量关系的工具,增加对一元二次方程的感性认识。学情分析:此知识是在学生学习了一元一次方程以及二元一次方程组等的基础上进一步对方程的学习,学生对方程并不陌生,学生在刚开始学习时会有一些困难,不少学生感觉一时还难以接受,因此他们方程理解也不可能是一蹴而就的,需要在研究实际问题的具体学习活动中反复不断地体验,逐步感受方程的意义。重点难点:一元二次方程的意义及一般形式,会正确识别一般式中的“项”及“系数”。教学过程一、复习引入:什么叫方程?什么叫一元一次方程?方程的“元”和“次”分别代表方程的什么?二、问题探究:1.根据题意列方程:(1)正方形桌面的面积是2m,求它的边长?解:设正方形桌面的边长是xm,根据题意,得(2)矩形花圃一面靠墙,另外三面所围的栅栏的总长度是19米。如果花圃的面积是24m2,求花圃的长和宽?11x解:设花圃的宽是xm,则花圃的长是(19-2x)m根据题意,得x(19-2x)=24整理的(3)我校图书馆的藏书在两年内从5万册增加到7.2万册,平均每年增长的百分率是多少?解:设平均每年增长的百分率是x根据题意,得整理,得(4)长5米的梯子斜靠在墙上,梯子的底端与墙的距离是3米。如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求梯子滑动的距离。解:设梯子滑动的距离是X米。根据勾股定理,滑动前梯子的顶端离地面4米,则滑动后梯子的顶端离地面(4-X)米,梯子的底端与墙的距离是(3+X)米。根据题意得整理。得2.观察上述所列的四个方程:;;;。它们是不是一元一次方程?有何共同点?请讨论总结:①;②;③。3.一元二次方程定义:像这样的等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程叫做225x43BAB'CA'X一元二次方程(quadraticequationinoneunknown)4.一般地,任何一个关于x的一元二次方程都可以化为(≠0)的形式,我们把(a,b,c为常数,a≠0)称为一元二次方程的一般形式。ax2二次项,a为二次项系数;bx一次项,b为一次项系数;为常数项。5.分别指出下列方程的二次项、二次项系数;一次项、一次项系数和常数项:三、精讲点拨:1.判断:下列方程中那些是二元一次方程:(只填序号)析:先看是否是整式方程,然后化简看是否只含有一个未知数,并且未知数的最高次数是22.将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:(1)(2)3.①关于的一元二次方程(+)++-=有一个解为0,求-的值。②关于的方程-(-)=+在什么条件下它是一元二次方程?在什么条件下它是一元一次方程?分析:根据一元二次方程的定义求解.四、反馈练习:课本P7练习133五、小结本课:1.只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程。2.一元二次方程的一般形式为(≠0),一元二次方程的项及系数都是根据一般式定义的,这与多项式中的项、次数及其系数的定义是一致的。3.在实际问题转化为数学模型(一元二次方程)的过程中,体会学习一元二次方程的必要性和重要性六、作业:P72P8习题1.11、24.1一元二次方程学案主备:张传美审核:李芳2010-11-1学习目标:1.通过观察,归纳一元二次方程的概念。2.理解掌握一元二次方程的一般形式(≠0)一、复习引入:什么叫方程?什么叫一元一次方程?方程的“元”445x43BAB'CA'和“次”分别指方程的什么?二、问题探究:1.根据题意列方程:(1)正方形桌面的面积是2m,求它的边长?解:设正方形桌面的边长是xm,根据题意,得(2)矩形花圃一面靠墙,另外三面所围的栅栏的总长度是19米。如果花圃的面积是24m2,求花圃的长和宽?解:设花圃的宽是xm,则花圃的长是m根据题意,得,整理得(3)我校图书馆的藏书在两年内从5万册增加到7.2万册,平均每年增长的百分率是多少?解:设平均每年增长的百分率是x根据题意,得,整理,得(4)长5米的梯子斜靠在墙上,梯子的底...