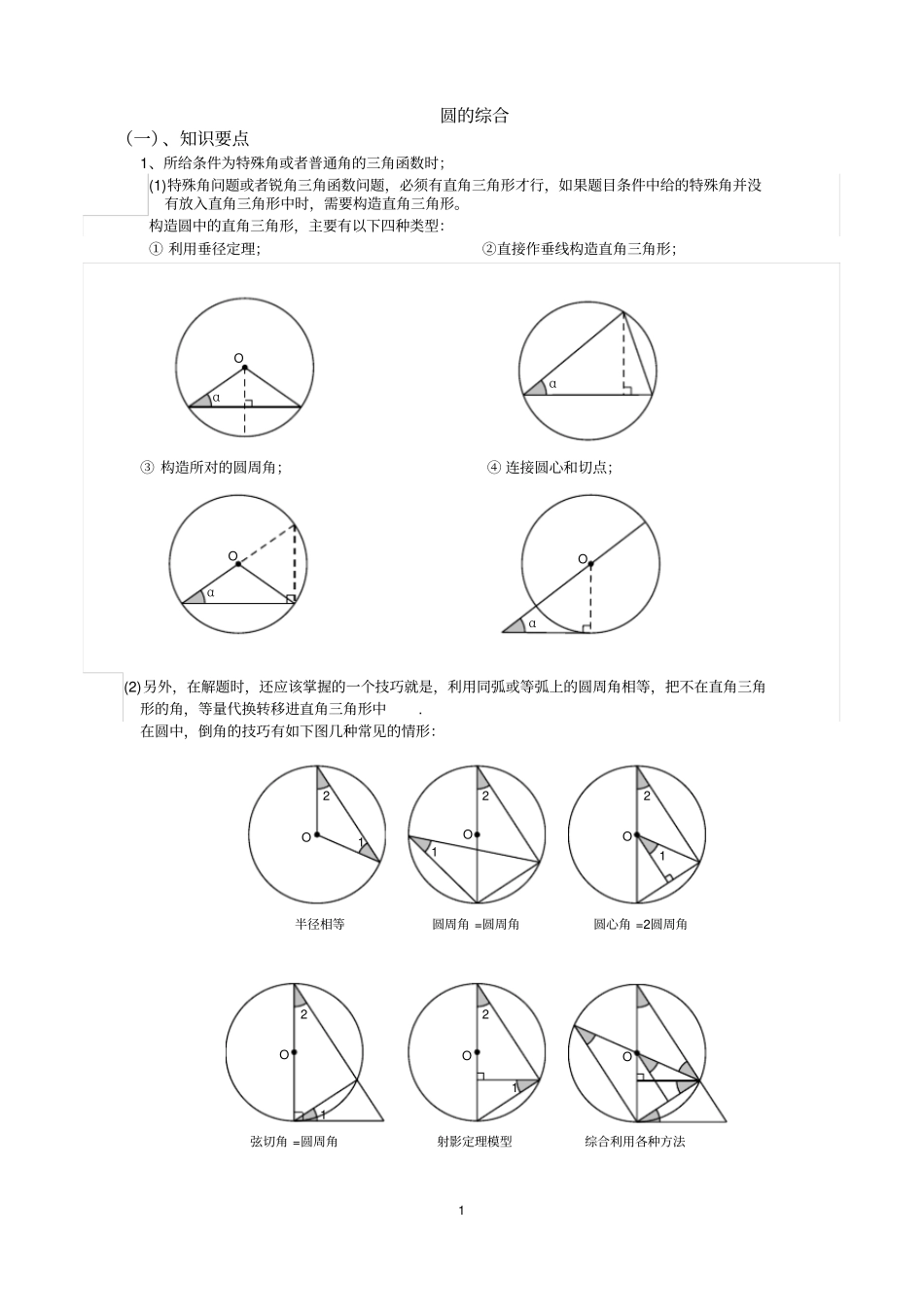
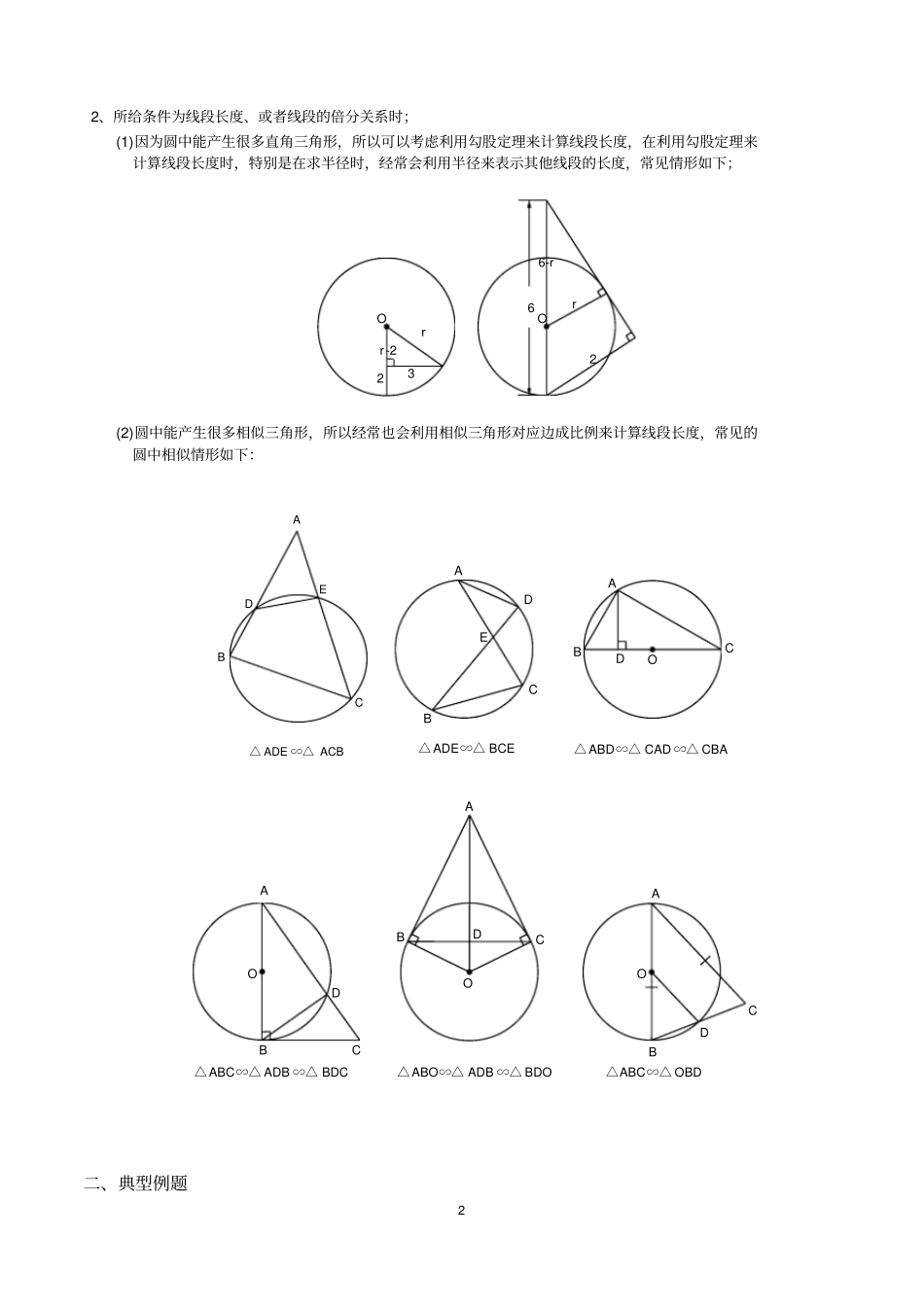
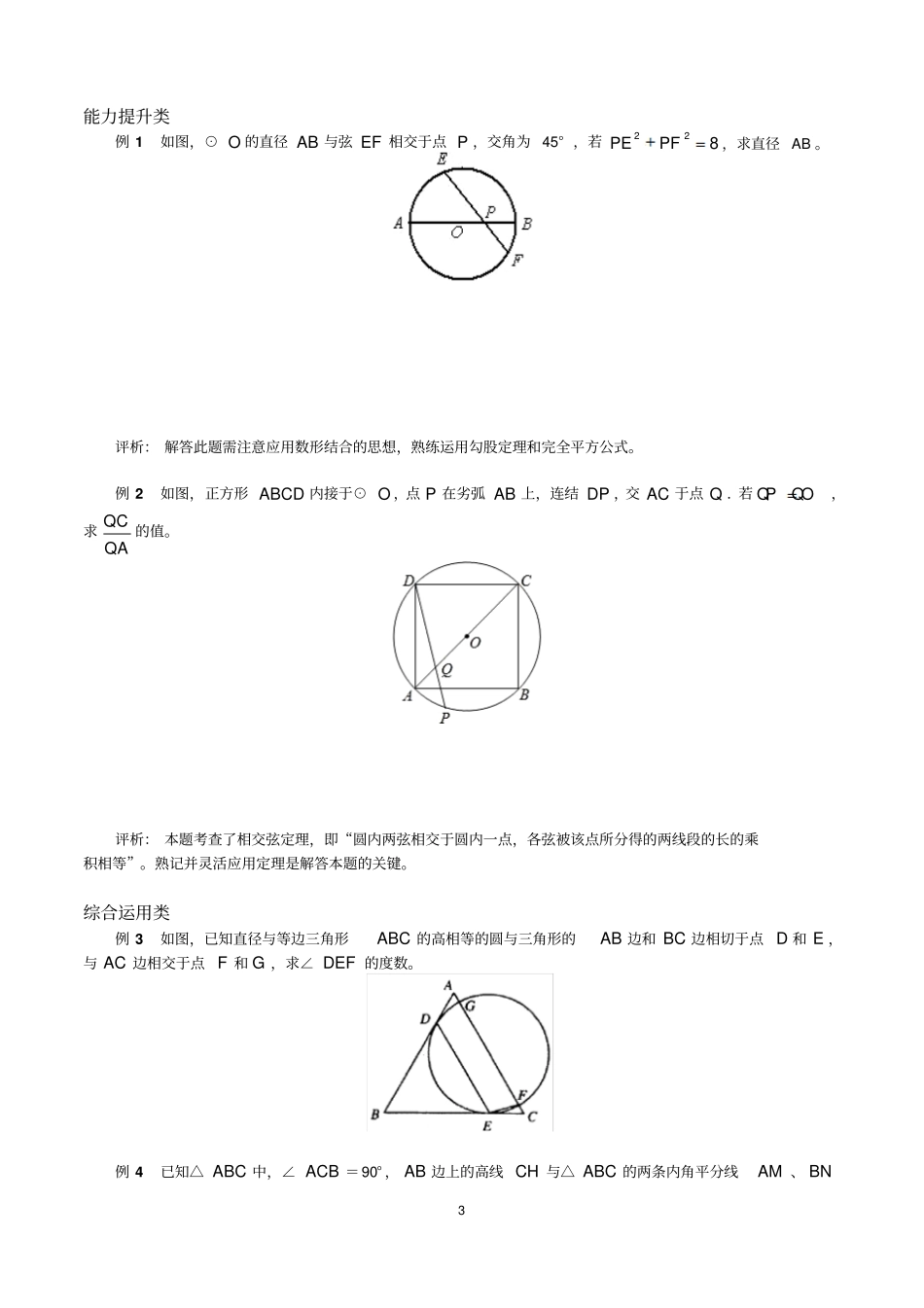
1圆的综合(一)、知识要点1、所给条件为特殊角或者普通角的三角函数时;(1)特殊角问题或者锐角三角函数问题,必须有直角三角形才行,如果题目条件中给的特殊角并没有放入直角三角形中时,需要构造直角三角形。构造圆中的直角三角形,主要有以下四种类型:①利用垂径定理;②直接作垂线构造直角三角形;α③构造所对的圆周角;④连接圆心和切点;Oα(2)另外,在解题时,还应该掌握的一个技巧就是,利用同弧或等弧上的圆周角相等,把不在直角三角形的角,等量代换转移进直角三角形中.在圆中,倒角的技巧有如下图几种常见的情形:半径相等12O圆周角=圆周角O12圆心角=2圆周角12O弦切角=圆周角O21射影定理模型O12综合利用各种方法OαOOα22、所给条件为线段长度、或者线段的倍分关系时;(1)因为圆中能产生很多直角三角形,所以可以考虑利用勾股定理来计算线段长度,在利用勾股定理来计算线段长度时,特别是在求半径时,经常会利用半径来表示其他线段的长度,常见情形如下;O3r-2r26r6-r2O(2)圆中能产生很多相似三角形,所以经常也会利用相似三角形对应边成比例来计算线段长度,常见的圆中相似情形如下:△ADE∽△ACBEDCBA△ADE∽△BCEEDCBA△ABD∽△CAD∽△CBACODAB△ABC∽△ADB∽△BDCBODAC△ABO∽△ADB∽△BDODOCBA△ABC∽△OBDODCBA二、典型例题3能力提升类例1如图,⊙O的直径AB与弦EF相交于点P,交角为45°,若228PEPF,求直径AB。评析:解答此题需注意应用数形结合的思想,熟练运用勾股定理和完全平方公式。例2如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连结DP,交AC于点Q.若QPQO,求QCQA的值。评析:本题考查了相交弦定理,即“圆内两弦相交于圆内一点,各弦被该点所分得的两线段的长的乘积相等”。熟记并灵活应用定理是解答本题的关键。综合运用类例3如图,已知直径与等边三角形ABC的高相等的圆与三角形的AB边和BC边相切于点D和E,与AC边相交于点F和G,求∠DEF的度数。例4已知△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的两条内角平分线AM、BN4分别交于P、Q两点,PM、QN的中点分别为E、F。求证:EF∥AB思维拓展类例5在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连结OD.(1)求b的值和点D的坐标;(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;(3)在(2)的条件下,如果以PD为半径的⊙P与⊙O外切,求⊙O的半径。评析:本题考查了运用待定系数法求函数解析式,同学们注意到分类讨论是解决本题的关键。例6已知AB为半圆O的直径,点P为直径AB上的任意一点.以点A为圆心,AP为半径作⊙A,⊙A与半圆O相交于点C;以点B为圆心,BP为半径作⊙B,⊙B与半圆O相交于点D,且线段CD的中5点为M.求证:MP分别与⊙A和⊙B相切。评析:这道题考查了相切两圆的性质和射影定理的应用,以及中位线的知识,对于这些重点知识,同学们应熟练掌握。总结:一、思想方法总结数形结合思想:将数与形结合起来进行分析、研究、解决问题的一种思想方法,特别是几何图形的直观性,能收到事半功倍的效果。转化思想:能将复杂图形转化为简单图形,将圆的有关计算问题转化为三角形、四边形的问题来解决。分类讨论思想:圆的有关概念、圆周角的有关求值及直线和圆、圆和圆的位置关系的讨论等问题均应用了这一思想。方程思想:在相交弦定理、切割线定理及弧长公式中,已知其他量,求一个量,运用了方程的思想。二、与圆有关的辅助线的添加规律:遇直径,作直径上的圆周角;遇切线,作过切点的半径或连结圆上某一点构成弦切角;证明圆周角相等,常用同弧上的圆心角过渡或作同弧上的圆周角;求弦长、弦心距、半径,常作垂直于弦的半径,连结圆心和弦的端点构造直角三角形;证明线段等积或成比例,一般构造相交弦、相交割线或相似三角形;遇到四个点在同一圆周上,要考虑到顺次连结四点构成圆内接四边形,再运用其性质解题;遇到圆外切三角形、多边形,应注意到切线长定理的应用。遇到两圆相交,添加公共弦或连心线,特别是公共弦,它在相交的两圆中起着桥梁...