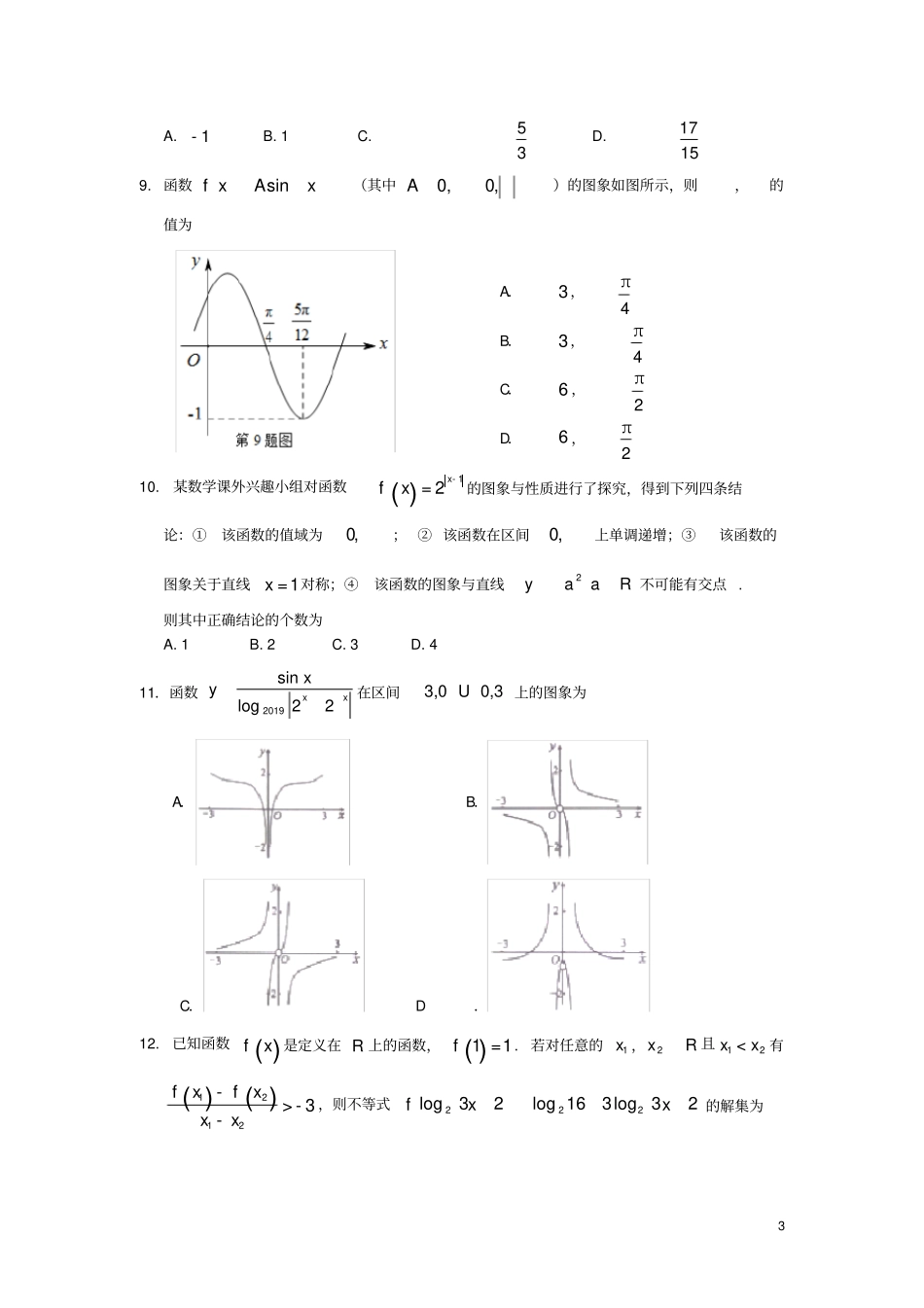
1学霸推荐学习十法一、听视并用法二、听思并用法三、五到听课法四、符号助记法五、要点记取法六、主动参与法七、听懂新知识法八、目标听课法九、质疑听课法十、存疑听课法2安庆市2019—2020学年度第一学期期末教学质量调研监测高一数学试题(考试时间:120分钟,满分:150分)第Ⅰ卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知全集{}235711131719U,,,,,,,=,集合{}2711A,,=,集合{}51113B,,=,则BACUA.{}5B.{}13C.{}513,D.{}1113,2.计算:33log2log6-=A.1B.1-C.3log2-D.32log2-3.已知幂函数axaaxf222在区间,0上是单调递增函数,则a的值为A.3B.1-C.3-D.14.在△ABC中,已知sin2sincosABC=,则此三角形一定为A.锐角三角形B.直角三角形C.等腰三角形D.钝角三角形5.若实数m,n满足22mn<,则下列不等关系成立的是A.22loglogmnn1D.33mn<6.下列关系式一定正确的是A.sin20C.()sinπ3sin3-=-D.sin22sin7.若函数sin2yx=的图象经过点()00Pxy,,则其图象必经过点A.()00,xy-B.00,2yxC.00,2yxD.()00πxy,-8.已知2tan,则2tan4tan3A.1-B.1C.53D.17159.函数xAxfsin(其中,0,0A)的图象如图所示,则,的值为A.3,π4B.3,π4C.6,π2D.6,π210.某数学课外兴趣小组对函数()12xfx-=的图象与性质进行了探究,得到下列四条结论:①该函数的值域为,0;②该函数在区间,0上单调递增;③该函数的图象关于直线1x=对称;④该函数的图象与直线Raay2不可能有交点.则其中正确结论的个数为A.1B.2C.3D.411.函数2019sinlog22xxxy在区间3,00,3U上的图象为A.B.C.D.12.已知函数()fx是定义在R上的函数,()11f=.若对任意的1x,Rx2且12xx<有()()12123fxfxxx->--,则不等式23log316log23log222xxf的解集为4A.1,32B.34,C.34,32D.,34第Ⅱ卷(非选择题)二、填空题:本大题共4小题,每小题5分,共20分,将答案填写在答题卷中的相应区域,答案写在试题卷上无效..........。13.函数()()2lg12fxxx=++-的定义域为______________.14.计算:21sin51sin21cos39sin.15.已知函数()2tan41xfxx=++,则()()()()()21012fffff-+-+++=________.16.若A为不等边△ABC的最小内角,则()2sincos1sincosAAfAAA=++的值域为____________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本题满分10分)已知集合1|xxA,集合RaaxaxB,33|.(Ⅰ)当4a=时,求ABU;(Ⅱ)若AB,求实数a的取值范围.18.(本题满分12分)已知角的顶点在坐标原点,始边与x轴非负半轴重合,终边经过点P()34,-.(Ⅰ)求cossin的值;(Ⅱ)求sin2cos2cossin的值.19.(本题满分12分)已知函数0cos6sinxxxf图象两条相邻对称轴间的距离为π2.(Ⅰ)求函数()fx在[]0π,上的单调递增区间;(Ⅱ)将函数()yfx=的图象向左平移π6个单位后得到函数()ygx=的图象,求函数()ygx=图象的对称中心坐标.20.(本题满分12分)5已知函数()24fxaxbx=++,其中Rba,,且0a.(Ⅰ)若函数()yfx=的图象过点()31,-,且函数()fx只有一个零点,求函数()fx的解析式;(Ⅱ)在(Ⅰ)的条件下,若Za,函数kxxfxgln在区间,2上单调递增,求实数k的取值范围.21.(本题满分12分)某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快.......开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积y(单位:平方米)与经过时间Nxx个月的关系有两个函数模型1,0akakyx与()0ypxqp=+>可供选择.(Ⅰ)试判断哪个函数模型更合适,并求出该模型的函数解析式;(Ⅱ)问约经过几个月,该水域中此生物的面积是当初投放的1000倍?(参考数据:48.03lg,30.02lg,73.13,41.12)22.(本题满分12分)已知函数1cos4sin22xxxf.(Ⅰ)当8,8x时,02mxmfxf恒成立,求实数m的取值范围;(Ⅱ)是否同时存在实数a和正整数n,使得函数()()gxfxa=-在[]0πn,上恰有2019个零点?若存在,请求出所有符合条件的a和n的值;若不存在,请说明理由.安庆市2019—2020学年度第一学期期末教学质量调研...