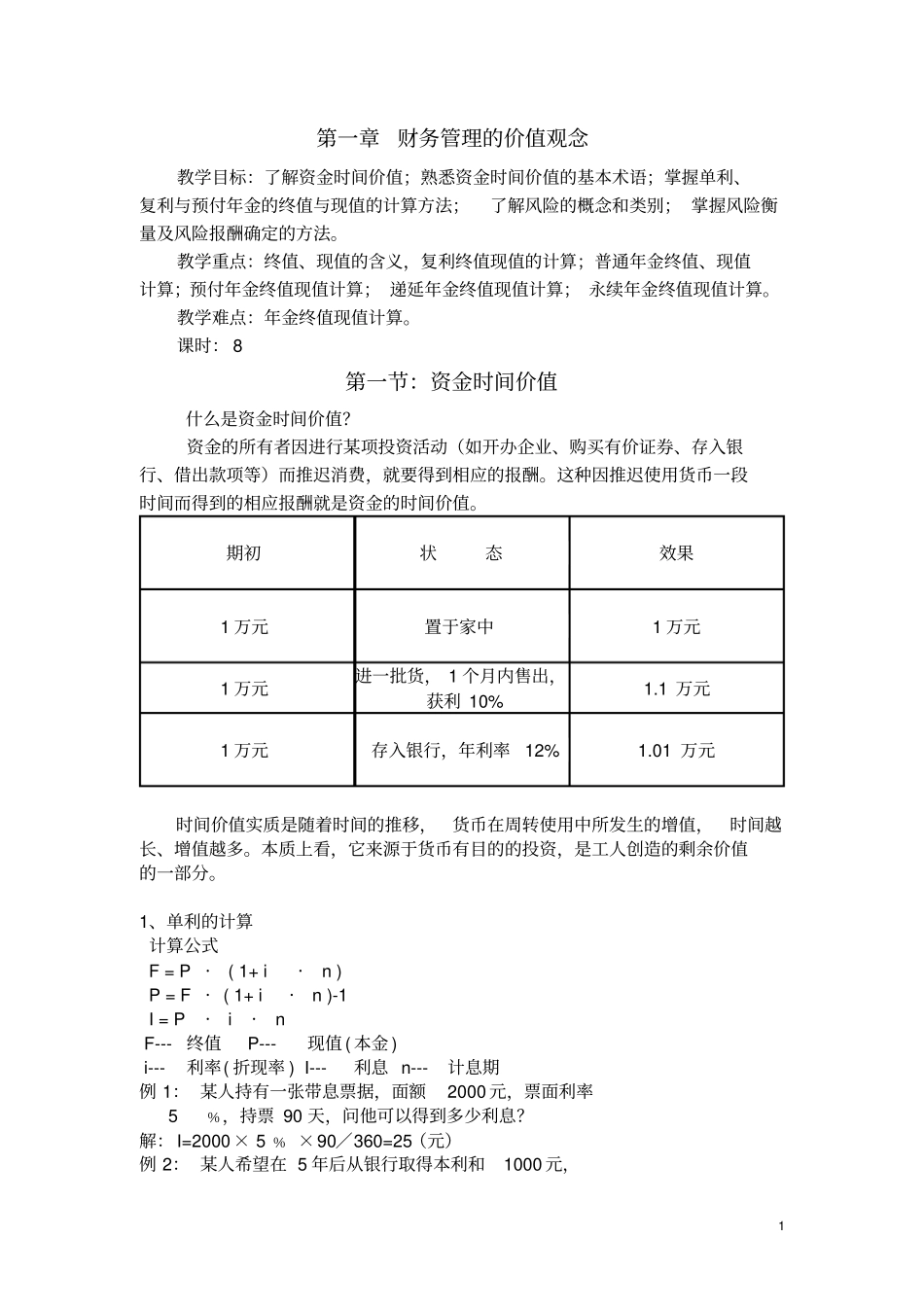
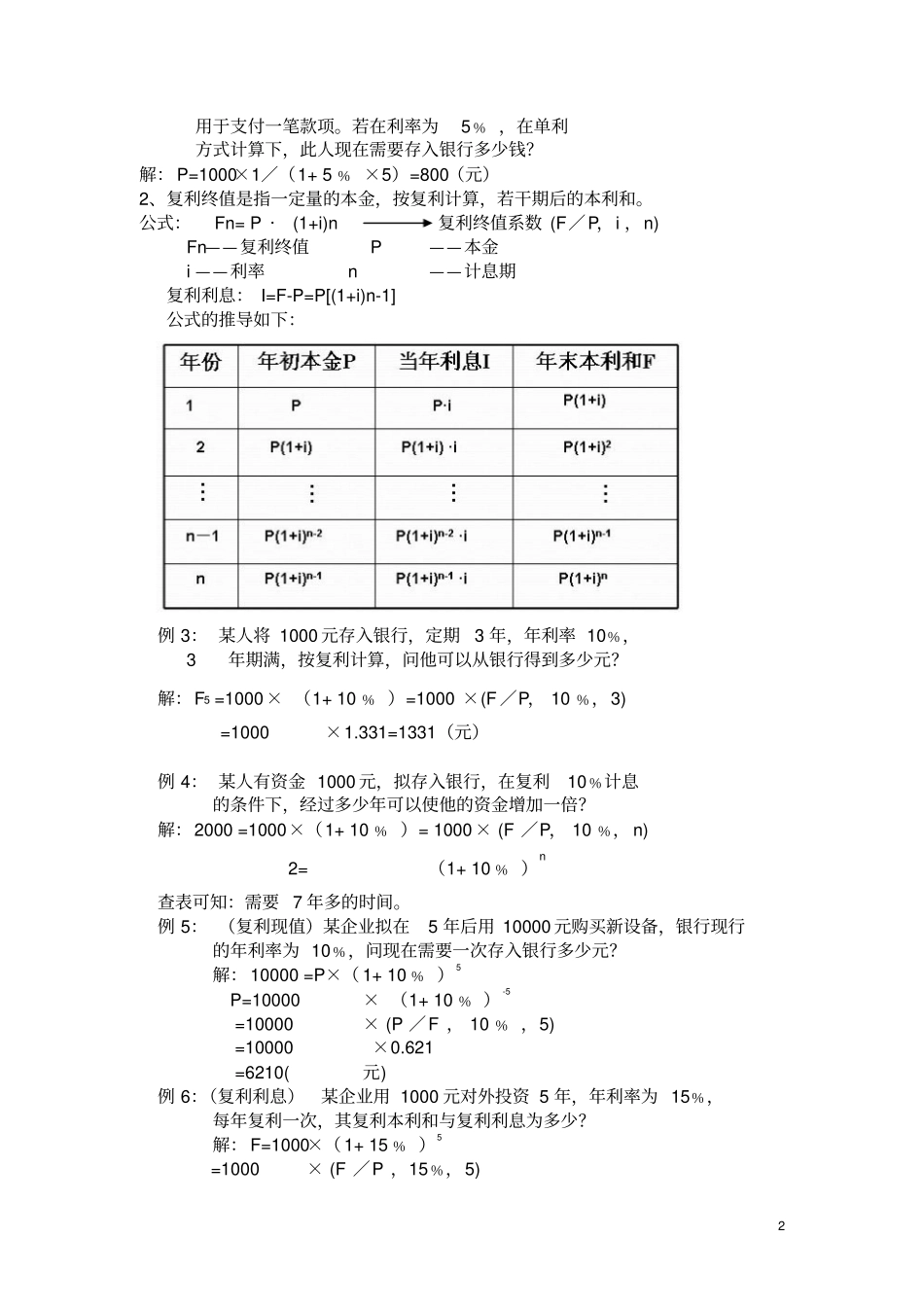
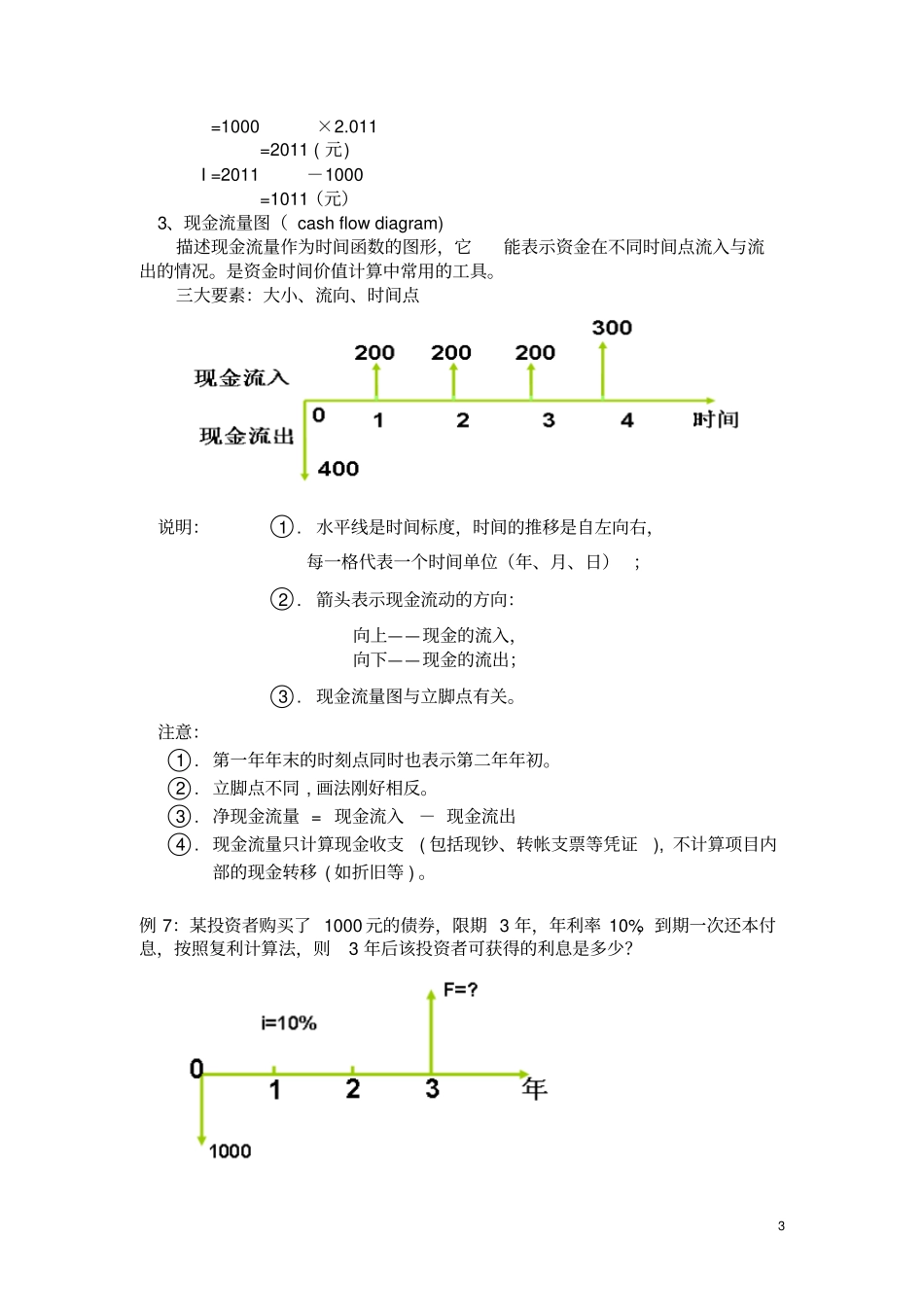
1第一章财务管理的价值观念教学目标:了解资金时间价值;熟悉资金时间价值的基本术语;掌握单利、复利与预付年金的终值与现值的计算方法;了解风险的概念和类别;掌握风险衡量及风险报酬确定的方法。教学重点:终值、现值的含义,复利终值现值的计算;普通年金终值、现值计算;预付年金终值现值计算;递延年金终值现值计算;永续年金终值现值计算。教学难点:年金终值现值计算。课时:8第一节:资金时间价值什么是资金时间价值?资金的所有者因进行某项投资活动(如开办企业、购买有价证券、存入银行、借出款项等)而推迟消费,就要得到相应的报酬。这种因推迟使用货币一段时间而得到的相应报酬就是资金的时间价值。期初状态效果1万元置于家中1万元1万元进一批货,1个月内售出,获利10%1.1万元1万元存入银行,年利率12%1.01万元时间价值实质是随着时间的推移,货币在周转使用中所发生的增值,时间越长、增值越多。本质上看,它来源于货币有目的的投资,是工人创造的剩余价值的一部分。1、单利的计算计算公式F=P·(1+i·n)P=F·(1+i·n)-1I=P·i·nF---终值P---现值(本金)i---利率(折现率)I---利息n---计息期例1:某人持有一张带息票据,面额2000元,票面利率5﹪,持票90天,问他可以得到多少利息?解:I=2000×5﹪×90∕360=25(元)例2:某人希望在5年后从银行取得本利和1000元,2用于支付一笔款项。若在利率为5﹪,在单利方式计算下,此人现在需要存入银行多少钱?解:P=1000×1∕(1+5﹪×5)=800(元)2、复利终值是指一定量的本金,按复利计算,若干期后的本利和。公式:Fn=P·(1+i)n复利终值系数(F∕P,i,n)Fn——复利终值P——本金i——利率n——计息期复利利息:I=F-P=P[(1+i)n-1]公式的推导如下:例3:某人将1000元存入银行,定期3年,年利率10﹪,3年期满,按复利计算,问他可以从银行得到多少元?解:F5=1000×(1+10﹪)=1000×(F∕P,10﹪,3)=1000×1.331=1331(元)例4:某人有资金1000元,拟存入银行,在复利10﹪计息的条件下,经过多少年可以使他的资金增加一倍?解:2000=1000×(1+10﹪)=1000×(F∕P,10﹪,n)2=(1+10﹪)n查表可知:需要7年多的时间。例5:(复利现值)某企业拟在5年后用10000元购买新设备,银行现行的年利率为10﹪,问现在需要一次存入银行多少元?解:10000=P×(1+10﹪)5P=10000×(1+10﹪)-5=10000×(P∕F,10﹪,5)=10000×0.621=6210(元)例6:(复利利息)某企业用1000元对外投资5年,年利率为15﹪,每年复利一次,其复利本利和与复利利息为多少?解:F=1000×(1+15﹪)5=1000×(F∕P,15﹪,5)3=1000×2.011=2011(元)I=2011-1000=1011(元)3、现金流量图(cashflowdiagram)描述现金流量作为时间函数的图形,它能表示资金在不同时间点流入与流出的情况。是资金时间价值计算中常用的工具。三大要素:大小、流向、时间点说明:○1.水平线是时间标度,时间的推移是自左向右,每一格代表一个时间单位(年、月、日);○2.箭头表示现金流动的方向:向上——现金的流入,向下——现金的流出;○3.现金流量图与立脚点有关。注意:○1.第一年年末的时刻点同时也表示第二年年初。○2.立脚点不同,画法刚好相反。○3.净现金流量=现金流入-现金流出○4.现金流量只计算现金收支(包括现钞、转帐支票等凭证),不计算项目内部的现金转移(如折旧等)。例7:某投资者购买了1000元的债券,限期3年,年利率10%,到期一次还本付息,按照复利计算法,则3年后该投资者可获得的利息是多少?4解:I=P[(1+i)n-1]=1000[(1+10%)3-1]=331元(三)年金的现值与终值?年金是(Annuity)指等额、定期的系列收支。特点:等额、等期形式:等期等额偿还贷款,等期等额发放养老金、等期等额支付工程款、每年相同的销售收入?按年金的收付时点,可以将年金划分为:普通年金、预付年金、递延年金、永续年金1、普通年金(OrdinaryAnnuity)又称后付年金:是指各期期末收付的年金。(1)普通年金终值:是一定时期内每期期末等额收付款项的复利终值之和。每期期末等额收付款项的复利终值之和普通年金终值计算公式的推导每年的支付金额为A;利率为I;期数为n;5则按复利计算的普...