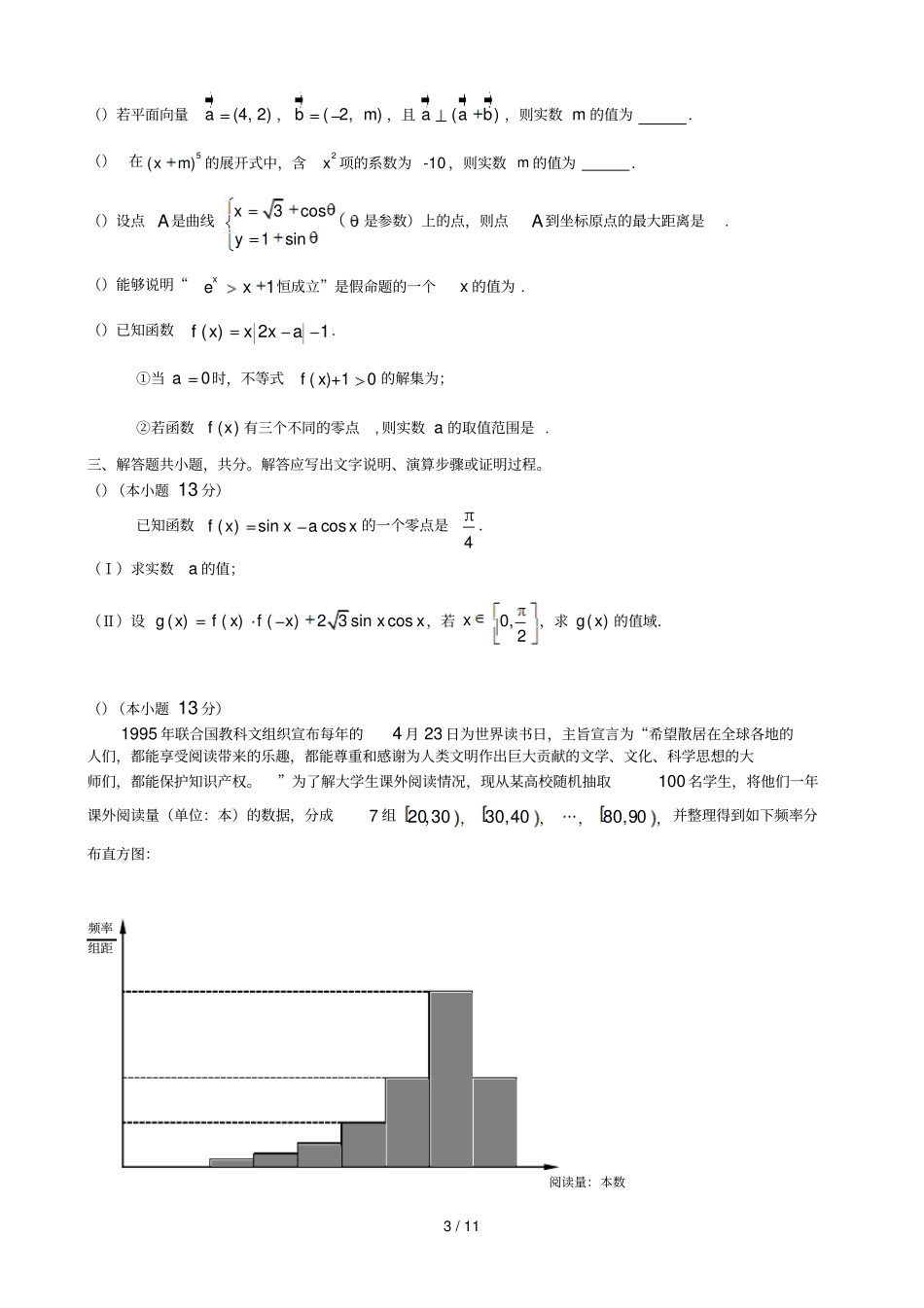
1/11房山区年高考第二次模拟测试试卷数学(理)本试卷共页,分。考试时长分钟。考生务必将答案答在答题纸上,在试卷上作答无效。考试结束后,将本试卷和答题纸一并交回。第一部分(选择题共40分)一、选择题共小题,每小题分,共分。在每小题列出的四个选项中,选出符合题目要求的一项。()设集合{|2},{|03}AxxBxx,则AB()2xx(){|3}xx(){|23}xx(){|23}xx()若复数iz1i,则复数z在复平面内对应的点位于()第一象限()第二象限()第三象限()第四象限()执行如图的程序框图,输出的S值为()65()64()63()33否输出结束是开始S1S1n2nSS1nn33?S2/11()已知实数,xy满足10,0,0,xyxy则22xy的取值范围是()01,()01,()1+,()2+2,()已知函数()fx的图像关于原点对称,且周期为,若(1)2f,则(2017)f()()2()0()2()4()已知某几何体的三视图如图所示,则该几何体的最长棱为()4()22()7()2()ABC的三个内角分别为A,B,C,则“=B3”是“A,B,C成等差数列”的()充分而不必要条件()必要而不充分条件()充要条件()既不充分也不必要条件()定义:若存在常数k,使得对定义域D内的任意两个1212,xxxx,均有1212fxfxkxx成立,则称函数fx在定义域D上满足利普希茨条件.若函数1fxxx满足利普希茨条件,则常数k的最小值为()4()3()1()12第二部分(非选择题共110分)二、填空题共小题,每小题分,共分。()设双曲线222210,0xyabab的一条渐近线方程为20xy,则该双曲线的离心率为.俯视图3左视图主视图3/11()若平面向量(4,2)a,(2,)bm,且()aab,则实数m的值为.()在5()xm的展开式中,含2x项的系数为-10,则实数m的值为.()设点A是曲线3cos1sin(xy是参数)上的点,则点A到坐标原点的最大距离是.()能够说明“xe1x恒成立”是假命题的一个x的值为.()已知函数()21fxxxa.①当0a时,不等式()+10fx的解集为;②若函数()fx有三个不同的零点,则实数a的取值范围是.三、解答题共小题,共分。解答应写出文字说明、演算步骤或证明过程。()(本小题13分)已知函数()sincosfxxax的一个零点是π4.(Ⅰ)求实数a的值;(Ⅱ)设()()()23sincosgxfxfxxx,若x0,2,求()gx的值域.()(本小题13分)1995年联合国教科文组织宣布每年的4月23日为世界读书日,主旨宣言为“希望散居在全球各地的人们,都能享受阅读带来的乐趣,都能尊重和感谢为人类文明作出巨大贡献的文学、文化、科学思想的大师们,都能保护知识产权。”为了解大学生课外阅读情况,现从某高校随机抽取100名学生,将他们一年课外阅读量(单位:本)的数据,分成7组2030,,30,04,,80,09,并整理得到如下频率分布直方图:阅读量:本数频率组距4/11(Ⅰ)估计其阅读量小于60本的人数;(Ⅱ)已知阅读量在2030,,30,04,4050,内的学生人数比为2:3:5.为了解学生阅读课外书的情况,现从阅读量在20,04内的学生中随机选取3人进行调查座谈,用X表示所选学生阅读量在2030,内的人数,求X的分布列和数学期望;(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计100名学生该年课外阅读量的平均数在第几组(只需写出结论).()(本小题14分)如图1,正六边形ABCDEF的边长为2,O为中心,G为AB的中点.现将四边形DEFC沿CF折起到四边形11DEFC的位置,使得平面ABCF平面11DEFC,如图2.(Ⅰ)证明:1DF平面1EOG;(Ⅱ)求二面角1EOGF的大小;(Ⅲ)在线段1CD上是否存在点H,使得//BH平面1EOG?如果存在,求出11DHDC的值;如果不存在,请说明理由.()(本小题13分)设函数()lnfxxkx,(k为常数),xfxxxg11.曲线xfy在点1,1f处的切线与x轴平行.(Ⅰ)求k的值;(Ⅱ)求gx的单调区间和最小值;ABCDEFG.O图1图21EBC1DAFOG5/11(Ⅲ)若axgag1)()(对任意0x恒成立,求实数a的取值范围.()(本小题14分)已知椭圆222210:xyCabab的离心率为12,O为坐标原点,F是椭圆C的右焦点,A为椭圆C上一点,且AFx轴,AFO的面积为34.(Ⅰ)求椭圆C的方程;(Ⅱ)过C上一点000,0Pxyy的直线l:00221xxyyab与直线AF相交于点M,与直线4x相交于点N.证明:当点P在C上移动时,MFNF恒为定值,并求此定值.(20)(本小题...