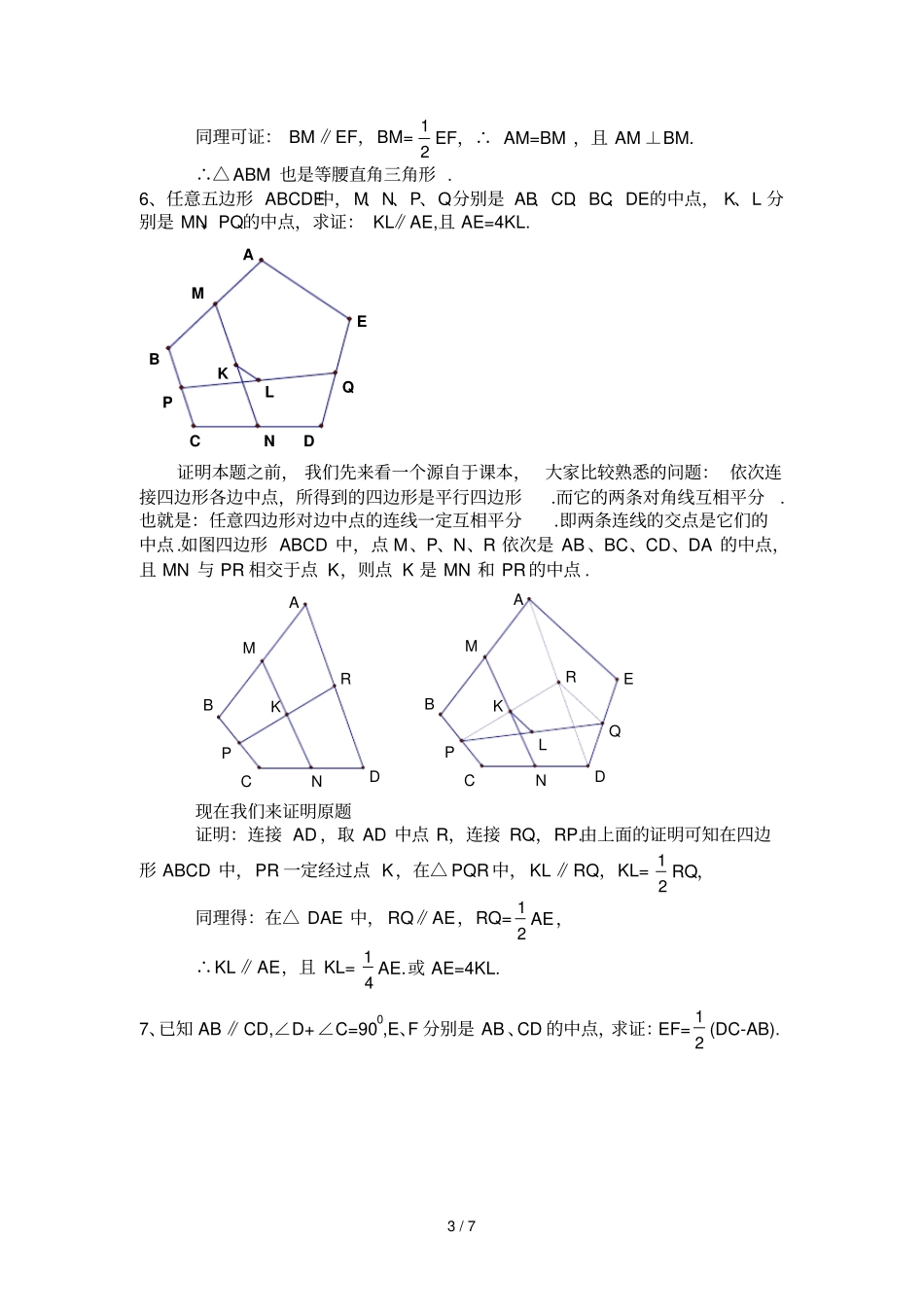
1/7本文为自本人珍藏版权所有仅供参考中位线问题集1、如图,四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD分别交于点E、F.试说明∠BEN=∠NFC.FENMABCD21GFEMNBCDA证明:连接BD,取BD中点G,连接GM,GN.在△ABD中MG∥AB,且MG=21AB,同理:NG∥CD,NG=21CD∴∠1=∠BEN,∠2=∠CFN AB=CD,∴GM=GN,∴∠1=∠2,∴∠BEN=∠CFN本题证明的方法很多,由于大家都比较熟悉,很多参考资料上都有,故不再例举.2、△ABC中,中线BD、CE相交于点O,F、G分别是OB、OC的中点,求证:四边形EFGH是平行四边形.你还能得到什么结论?FGOEDABC证明:在△ABC,ED=21BC,且ED∥BC在△OBC中FG=21BC,且FG∥BC∴ED∥FG,ED=FG,∴平行四边形DEFG.3、梯形ABCD中,AD∥BC,E是腰AB的中点,且DE⊥CE.求证:DE、EC分别平分∠ADC和∠BCD.2/7AEDBC321FDEBCA证明:取CD中点F,连接EF.∴EF∥AD,∠1=∠3,在Rt△CDE中,FE=FD,∴∠2=∠3∠1=∠2,即DE平分∠ADC,同理,CE平分∠BCD.此讲义针对中位线,其他方法不再例举,4、如图,E、F分别是梯形ABCD的对角线中点,求证:)(21ADBCEFFEDBCAGFEBCDA证明:连接DF并延长交BC于点G,易证得:△ADF≌△CGF,∴FD=FG,AD=CG,在△DBG中,EF=21BG=21(BC-AD).5、分别以△ABC的AC、BC为腰,A、B为顶点做等腰直角△ACE、△BCD,M为DE中点,求证:△ABM也是等腰直角三角形.MDEABCGFMDEABC证明:延长EA到F,使AF=AE,连接CF,延长DB到G,使BG=BD,连接CG.连接EG,DF.易证得:△ECG≌△FCD,(实际上是将△ECG绕点C旋转90°得到△FCD).∴EG=FD,在△EDF中,AM为中位线,∴AM∥DF,AM=21DF,3/7同理可证:BM∥EF,BM=21EF,∴AM=BM,且AM⊥BM.∴△ABM也是等腰直角三角形.6、任意五边形ABCDE中,M、N、P、Q分别是AB、CD、BC、DE的中点,K、L分别是MN、PQ的中点,求证:KL∥AE,且AE=4KL.KLMNPQABCDE证明本题之前,我们先来看一个源自于课本,大家比较熟悉的问题:依次连接四边形各边中点,所得到的四边形是平行四边形.而它的两条对角线互相平分.也就是:任意四边形对边中点的连线一定互相平分.即两条连线的交点是它们的中点.如图四边形ABCD中,点M、P、N、R依次是AB、BC、CD、DA的中点,且MN与PR相交于点K,则点K是MN和PR的中点.RKPMNCDABRKLQPMNCDEAB现在我们来证明原题证明:连接AD,取AD中点R,连接RQ,RP.由上面的证明可知在四边形ABCD中,PR一定经过点K,在△PQR中,KL∥RQ,KL=21RQ,同理得:在△DAE中,RQ∥AE,RQ=21AE,∴KL∥AE,且KL=41AE.或AE=4KL.7、已知AB∥CD,∠D+∠C=900,E、F分别是AB、CD的中点,求证:EF=21(DC-AB).4/7EBFDCAHGEBFDCA证明:过点D作DG∥BC,交BF的延长线于点G,连接AG,DC于点H.易证得:△BCF≌△DGF,∴BF=FG,在△ABG中,EF=21AG,EF∥AG,又 AB∥CD,∴四边形AEFH是平行四边形.EF=AH,且EF=21AG,∴点H为AG的中点.在△ADG中, DG∥BC且BC⊥AD,∴DG⊥AD,DH=21AG=EF,而EF=DH=DF–AE=21(DC–AB).本题也有多种证法,不再例举.8、在等腰三角形ABC的两腰AB、AC上分别取点E和F,使AE=CF,已知BC=2,证明:EF≥1.FBCAE在证明本题之前,我们也来看一条大家比较熟悉的问题:在△AMN中,AM=AN,点E是AM上一点,点F是AN延长线上的一点,EF与BC相交于点D,且EM=FN,求证:ED=DFGDFMNAE证明:过点E作EG∥AF,交MN于点G,易证得:△EGD≌△FND,∴DE=DF5/7321HGDNMBCAEF现在我们来证明原题.证明:①当E、F分别为AB、AC中点时:EF=21BC=1;②当E、F与不是AB、AC中点时:取AB、AC中点M、N,连接MN,交EF于D, AB=AC,∴AM=CN,又 AE=CF,∴EM=FN,由前面的说明可得:DE=DF.过点E作EG∥MN,交AC于点H,过点F作FG⊥EG,垂足为G,连接GD、GN,在中,点D为EF中点,∴DG=DF,在Rt△FGH中,GN为斜边FH上的中线,故NG=NH,∴∠NGH=∠1=∠3=∠1,∴NG∥ME,又 EG∥MN,∴四边形EMNG是平行四边形,∴EG=MN,在△DEG中,DE+DG>EG,即:EF>MN,∴EF>1,综合①、②可得:EF≥1.感觉这种方法较麻烦,不知老师们是否有更为简便的证法.(征集中)9、△ABC中,∠B,∠C的平分线BE,CF相交于O,AG⊥BE于G,AH⊥CF于H.(1)求证:(1)GH∥BC;(2)若AB=9厘米,AC...