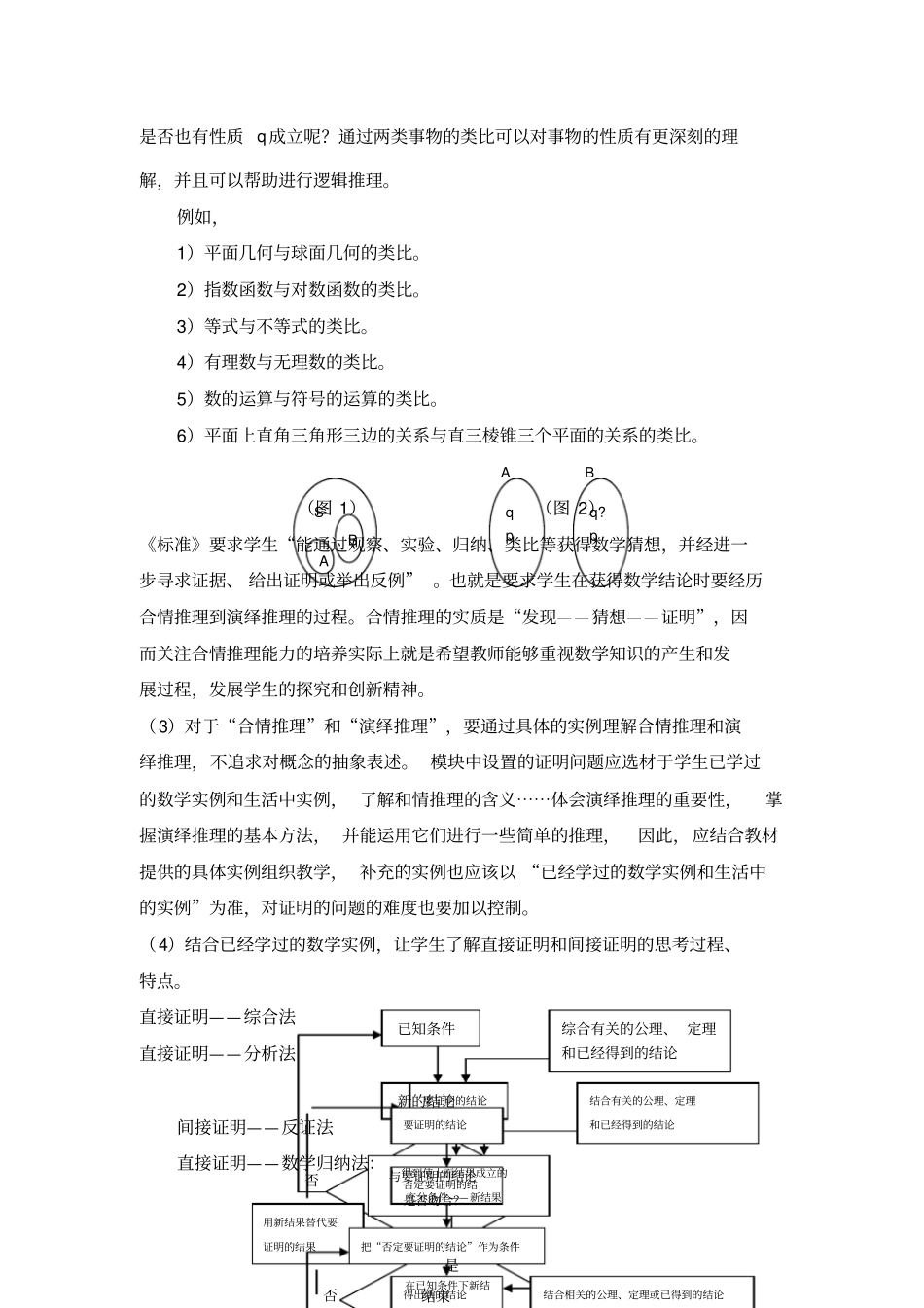
数学选修2——2课标解读2.2推理与证明1.知识内容的整体定位“推理与证明”是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理与演绎推理。合情推理是根据已有的事实和正确的结论(包括定义、公理、定理)、试验和实践的结果,以及个人的经验和直觉等推测某些结果的推理过程,归纳、类比是合情推理常用的思维方法。在解决问题的过程中,合情推理具有猜测和发现结论、探索和提供思路的作用,有利于创新意识的培养。演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等),按照严格的逻辑法则得到新的结论的推理过程,培养和提高学生的演绎推理或逻辑证明的能力是高中数学课程的重要目标。合情推理和演绎推理之间联系紧密、相辅相成。证明包括逻辑证明和试验、实践证明,数学结论的正确性必须通过逻辑证明来保证,即在前提正确的基础上,通过正确使用推理规则得出结论。在本模块中,学生将通过对已学过知识的回顾,进一步体会合情推理、演绎推理以及二者之间的联系与差异;体会数学证明的特点,了解数学证明的基本方法,包括直接证明的方法(如分析法、综合法)和间接证明的方法(如反证法);感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯。为了更好地理解整体定位,需要明确以下几个方面的问题:(1)归纳推理归纳推理是针对一类事物而言的,如图(1)所示:A和B具有的共同的特性是否可以推广到整个S?这就是一个从局部到整体的过程。例如,1)在统计学中,由一部分数据的特征数,推测出总体数据的特征数。2)解线性方程组时,由二元线性方程组的解法,推广到多元线性方程组的解法。3)平面向量推广到空间向量再推广到向量空间。(2)类比推理类比推理是针对的两类事物,如图(2)所示,在A和B两类事物中,A类中有性质p成立,B类中也有性质p成立,A类中还有性质q成立,那么B类中是否也有性质q成立呢?通过两类事物的类比可以对事物的性质有更深刻的理解,并且可以帮助进行逻辑推理。例如,1)平面几何与球面几何的类比。2)指数函数与对数函数的类比。3)等式与不等式的类比。4)有理数与无理数的类比。5)数的运算与符号的运算的类比。6)平面上直角三角形三边的关系与直三棱锥三个平面的关系的类比。(图1)(图2)《标准》要求学生“能通过观察、实验、归纳、类比等获得数学猜想,并经进一步寻求证据、给出证明或举出反例”。也就是要求学生在获得数学结论时要经历合情推理到演绎推理的过程。合情推理的实质是“发现——猜想——证明”,因而关注合情推理能力的培养实际上就是希望教师能够重视数学知识的产生和发展过程,发展学生的探究和创新精神。(3)对于“合情推理”和“演绎推理”,要通过具体的实例理解合情推理和演绎推理,不追求对概念的抽象表述。模块中设置的证明问题应选材于学生已学过的数学实例和生活中实例,了解和情推理的含义⋯⋯体会演绎推理的重要性,掌握演绎推理的基本方法,并能运用它们进行一些简单的推理,因此,应结合教材提供的具体实例组织教学,补充的实例也应该以“已经学过的数学实例和生活中的实例”为准,对证明的问题的难度也要加以控制。(4)结合已经学过的数学实例,让学生了解直接证明和间接证明的思考过程、特点。直接证明——综合法直接证明——分析法间接证明——反证法直接证明——数学归纳法:SABqpq?pAB已知条件新的结论与要证明的结论是否吻合?结束综合有关的公理、定理和已经得到的结论是否要证明的结论得到使上面结果成立的充分条件——新结果在已知条件下新结结合有关的公理、定理和已经得到的结论否用新结果替代要证明的结果要证明的结论否定要证明的结把“否定要证明的结论”作为条件得出新的结论结合相关的公理、定理或已得到的结论《标准》对“了解和情推理的含义,能利用归纳和类比等进行简单的推理;了解直接证明的两种基本方法和间接证明的一种方法”的要求是阶段性要求,“体会并认识合情推理在数学发现中的作用,感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯”的要求是终结性要求。2.课程标准的要求(1)合情推理...