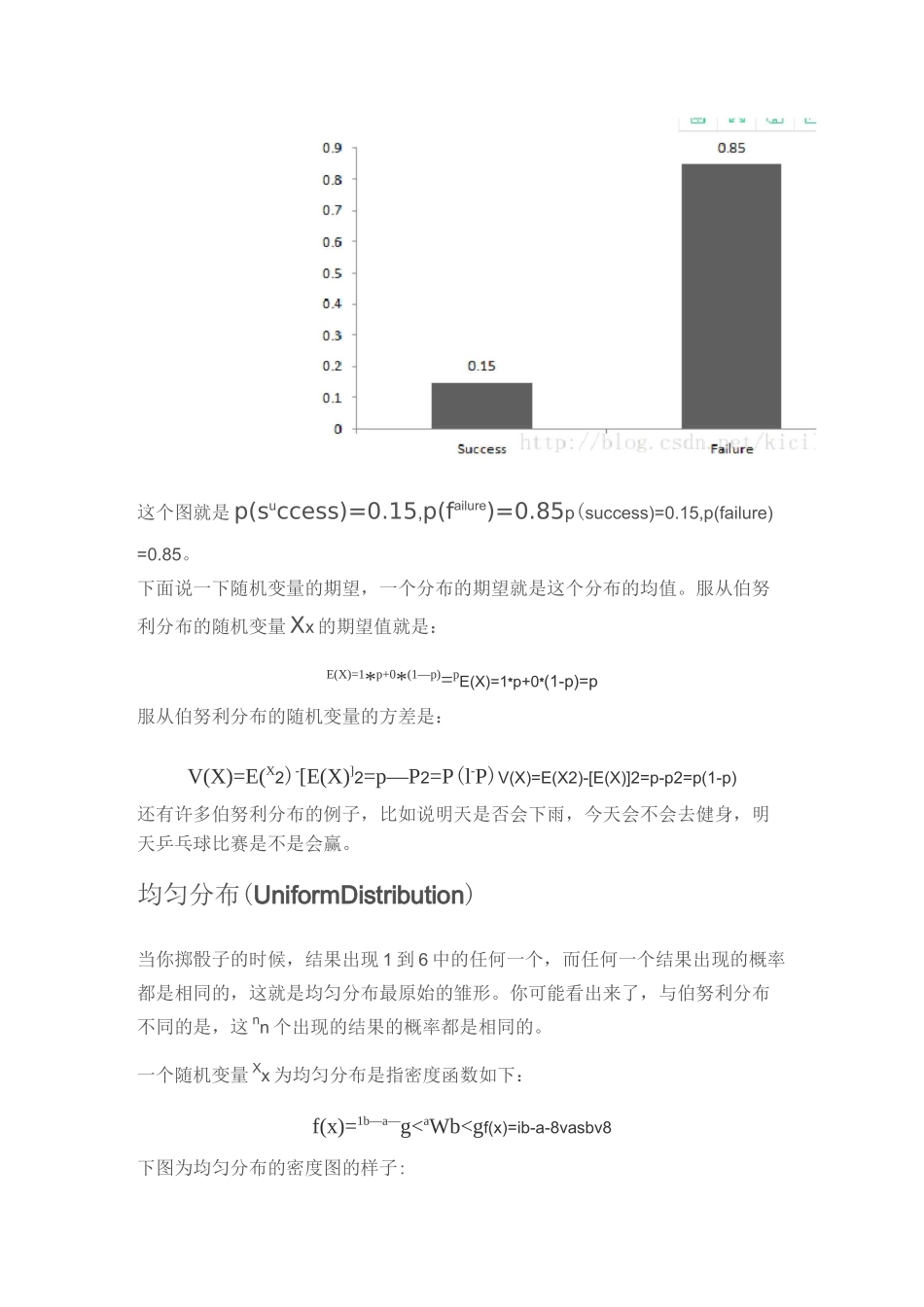
一、常见数据类型在正式的解释分布之前,我们先来看一看平时遇到的数据。数据可大致分为离散型数据和连续型数据。离散型数据离散型数据顾名思义就是只取几个特定的值。例如:当你掷骰子的时候,结果只有1,234,5,6,不会出现类似1.5,2.5。连续型数据在一个给定的范围内,连续型数据可以取任意值。这个范围可以是有限的或者是无穷的。例如:一个人的体重或者身高,可以取值54kg,54.4kg,54.33333kg等等都没有问题。下面就开始介绍分布的类型。二、分布类型伯努利分布(BernoulliDistribution)首先从最简单的分布开始,伯努利分布实际上是一个听起来最容易理解的分布。伯努利分布一次实验有两个可能的结果,比如1代表success及0代表failure。随机变量Xx—个取值为1并代表成功,成功概率为Pp,—个取值为0表示失败,失败概率为qq或者说l-p1-p。这里,概率分布函数为Px(l-P)l-xpx(1-p)1-x,其中xU(°'l)xw(0,1),我们也可以写成如下形式:P(x)={l-p,p,x=0x=1P(x)={1-p,x=0p,x=1成功和失败的概率没必要相同,也就是没必要都是0.5,但是这俩概率加和应该为1,比如可以是下面的图:这个图就是p(success)=0.15,p(failure)=0.85p(success)=0.15,p(failure)=0.85。下面说一下随机变量的期望,一个分布的期望就是这个分布的均值。服从伯努利分布的随机变量Xx的期望值就是:E(X)=1*p+0*(1—p)=pE(X)=1*p+0*(1-p)=p服从伯努利分布的随机变量的方差是:V(X)=E(X2)-[E(X)]2=p—P2=P(l-P)V(X)=E(X2)-[E(X)]2=p-p2=p(1-p)还有许多伯努利分布的例子,比如说明天是否会下雨,今天会不会去健身,明天乒乓球比赛是不是会赢。均匀分布(UniformDistribution)当你掷骰子的时候,结果出现1到6中的任何一个,而任何一个结果出现的概率都是相同的,这就是均匀分布最原始的雏形。你可能看出来了,与伯努利分布不同的是,这nn个出现的结果的概率都是相同的。一个随机变量Xx为均匀分布是指密度函数如下:f(x)=1b—a—g
E(X)=(a+b)2E(X)=(a+b)2Variance->V(X)=(b-a)2l2V(X)=(b-a)212标准的均匀分布的密度参数为a=°a=0和b=°b=0,所以对于标准的均匀分布的密度函数为:f(x)={1,0,0