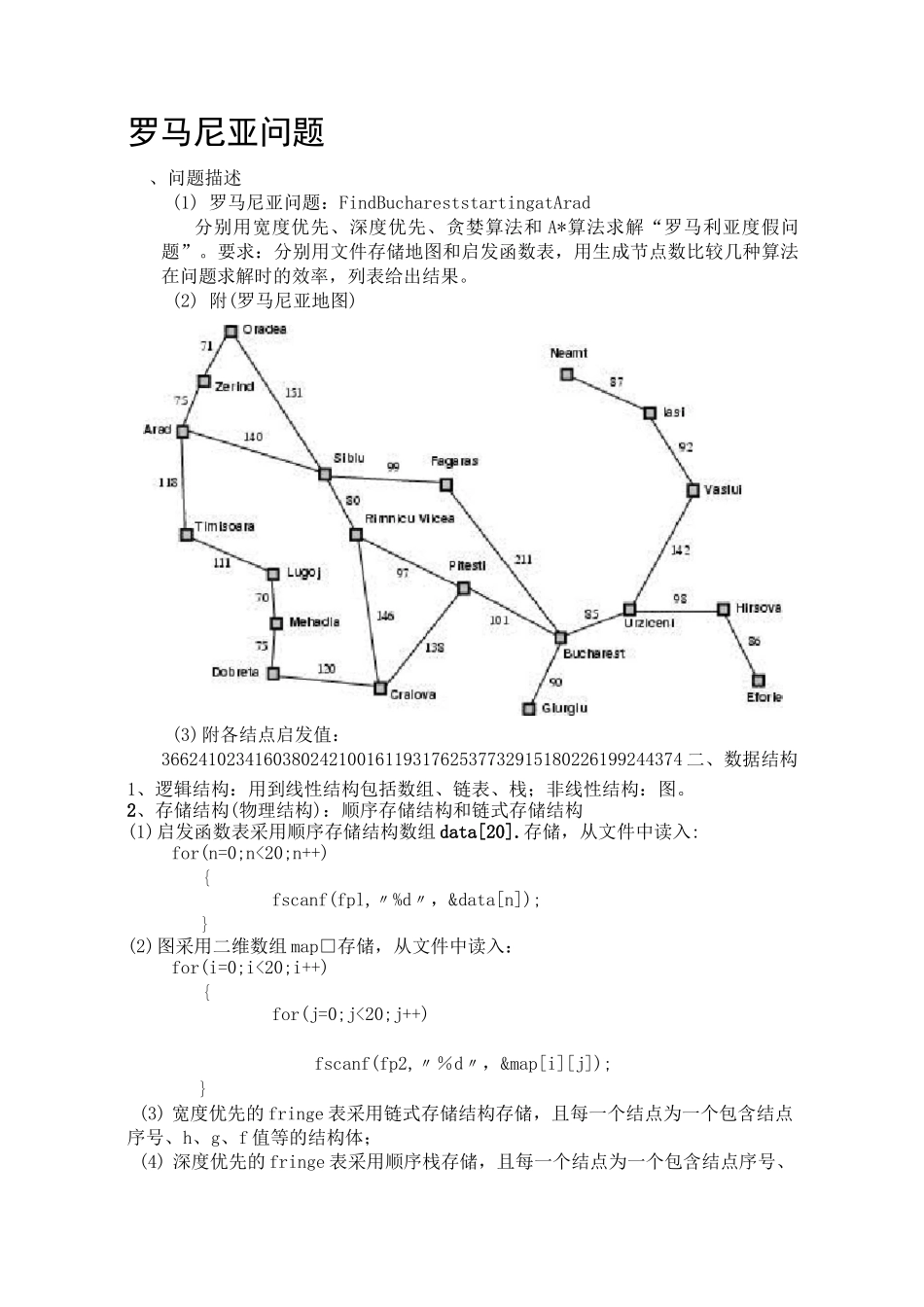
罗马尼亚问题、问题描述(1)罗马尼亚问题:FindBuchareststartingatArad分别用宽度优先、深度优先、贪婪算法和A*算法求解“罗马利亚度假问题”。要求:分别用文件存储地图和启发函数表,用生成节点数比较几种算法在问题求解时的效率,列表给出结果。(2)附(罗马尼亚地图)(3)附各结点启发值:36624102341603802421001611931762537732915180226199244374二、数据结构1、逻辑结构:用到线性结构包括数组、链表、栈;非线性结构:图。2、存储结构(物理结构):顺序存储结构和链式存储结构(1)启发函数表采用顺序存储结构数组data[20].存储,从文件中读入:for(n=0;n<20;n++){fscanf(fpl,〃%d〃,&data[n]);}(2)图采用二维数组map□存储,从文件中读入:for(i=0;i<20;i++){for(j=0;j<20;j++)fscanf(fp2,〃%d〃,&map[i][j]);}(3)宽度优先的fringe表采用链式存储结构存储,且每一个结点为一个包含结点序号、h、g、f值等的结构体;(4)深度优先的fringe表采用顺序栈存储,且每一个结点为一个包含结点序号、h、g、f值等的结构体;(5)贪婪算法和A*算法采用结构体数组存储。3、数据的运算:抽象数据类型(1)定义typedefstructfringe{intstate;//存储点序号信息intg;//g值inth;//h值intf;//f值intk;//标记是否已扩展}FringeType;(2)运算:检索、插入、删除等运算(3)表示:每一个数据元素就是一个记录。它包括学生的结点序号信息、g值、h值、f值等数据项,在解决实际应用问题时把每个记录当作一个基本单位进行访问和处理。三、算法思想1、宽度优先(1)算法描述:从Arad结点出发,判断是否为目标结点,若否,宽度优先搜索系统地探寻与该结点相连的结点,算法首先搜索和Arad距离为k的所有顶点,然后再去搜索和Arad距离为k+l的其他顶点,找出并存进待扩展结点表,等待扩展,每次先判断待扩展结点表是否为空,若否则从待扩展结点表中取出一个结点进行扩展,并将扩展后的结点存进该表,若是,则返回失败。该算法同时能生成一棵根为Arad且包括所有可达顶点的宽度优先树。宽度优先算法一直通过已找到和未找到顶点之间的边界向外扩展。通过为每个顶点着色(白色、灰色和黑色)。算法开始前所有顶点都是白色,随着搜索的进行,各顶点会逐渐被着色。在搜索中第一次碰到,着灰色,然后是灰色。因此,灰色和黑色顶点都已被发现,灰色顶点与一些白色顶点相邻接,它们代表着已找到和未找到顶点之间的边界。在宽度优先搜索中,我用到单链表来存储待扩展结点表。(2)伪代码实现:while(fringe[]!=NULL)takeoutu$fringe[]docoloru;while(uHgoal)doexpandu;BFS()for(1-20循环){if(有路径存在){新生成结点;BFSnode++;}}取链表的第一个结点;if(为goal){returnBFSnode;}elseif(不为goal){BFS();//递归调用}returnBFSnode;}putsuccessors(BFS)infringe[];end;end;(3)算法评价:宽度优先是完备的(如果分支因子有限的话),所以说,在任何情况下宽度优先都能找到一个解。此外,最坏的情况是,当目标结点是第d层的最后一个被扩展的结点时。时间复杂度:上「*_彳十…一*—匚二0片r(b为分支因子,d为深度)空间复杂度:所存储的节点的个数。2、深度优先(1)算法描述:深度优先搜索是一种每次都要达到被搜索结构的叶结点的搜索方法,直到不能再深入为止,然后返回到另一个结点,继续对该结点进行深搜。当有目标结点出现时,返回目标结点,搜索结束;否则,若待扩展结点表已空,且未找到目标结点,则返回失败,停止搜索。同样,深度优先搜索从Arad结点出发,判断是否为目标结点,若否,探寻与该结点相连的结点,算法首先搜索一条分支上的所有顶点,然后再去搜索和Arad的其它分支结点,找出并存进待扩展结点表,等待扩展,每次先判断待扩展结点表是否为空,若否,则从待扩展结点表中取出一个结点进行扩展,并将扩展后的结点存进该表,若是,则返回失败。该算法同时能生成一棵根为Arad且包括所有可达顶点的深度优先树。在深度优先搜索中,我用到堆栈来存储待扩展结点表。(2)伪代码实现while(fringe[]!=NULL)takeoutu$fringe[]docoloru;while(uHgoal)doexpandu;DFS(){for(1-20循环){if(有路径存在){新生成结点;DFSnode++...