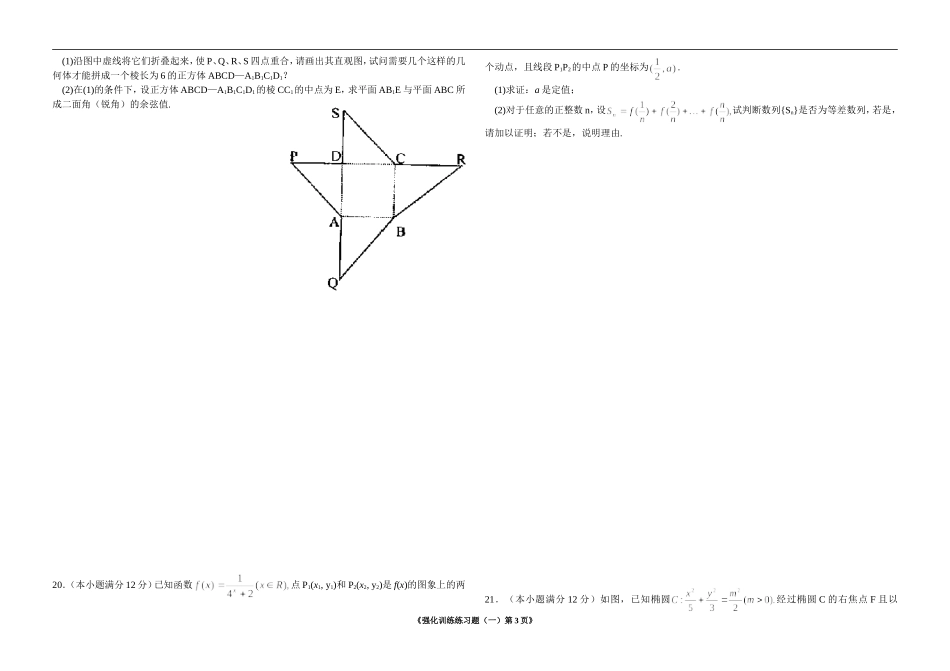
时0612182437体温(℃)37体温(℃)时0612182437时06121824体温(℃)37时06121824体温(℃)攀枝花市第十二中学校高2007级强化训练数学练习题(一)班级姓名总分一、选择题(本大题共12小题,每小题5分,共60分,将正确答案写在答题框内):1.设集合,为常数,且a,b不同时为零},则集合M∩P中的元素个数为A.0B.1C.2D.0或1或22.若是纯虚数,则的值为A.B.C.D.3.记二项式(1+2x)n展开式的各项系数和为an,其二项式系数和为bn,则等于A.-1B.1C.0D.不存在4.关于直线以及平面,下面命题中正确的是A、若则B、若则C、若且则D、若则5.某天清晨,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了.下面大致能上反映出小鹏这一天(0时—24时)体温的变化情况的图是ABCD6.已知,不等式的解集是,则满足的关系是A.B.C.D.7.若函数的图像关于点对称,且此函数的最小值为,则的一个可能的取值是A.0B.2C.3D.8.如图,目标函数的可行域为四边形OACB(含边界),若点C是该目标函数的唯一最优解,则的取值范围是A.B.C.D.9.方程曲线形状是10.关于函数,有下面四个结论:(1)是奇函数;(2)当时,恒成立;(3)的最大值是;(4)的最小值是.其中正确结论的个数是.A.1个B.2个C.3个D.0个11.已知定义在R上的偶函数f(x)的单调递减区间为[0,+∞,则不等式的解集是(A)(B)(C)(D)12.方程的根所在的区间是(A)(1,2)(B)(,)(C)(,)(D)(,)选择题答题框题号123456789101112答案二、填空题(本大题共4小题,每小题4分,共16分):《强化训练练习题(一)第1页》13.设函数在区间上连续,则实数a的值为;14.已知函数从小到大顺序为.15.的展开式中常数项是16.正六棱锥的侧棱长为2,底面边长为1,则侧棱与底面所成的角为.三、解答题(本大题共6小题,共84分):17.(本小题满分12分)某工厂准备将新开发的一种节能产品投入市场,在出厂前要对产品的四项质量指标进行严格的抽检.如果四项指标有两项指标不合格,则这批产品不能出厂.已知每项抽检是相互独立的,且每项抽检出现不合格的概率是.(1)求这批产品不能出厂的概率;(2)求直至四项指标全部检验完毕,才能确定该批产品能否出厂的概率.18.(本小题满分12分)平面直角坐标系内有点P(1)求向量的夹角的余弦用x表示的函数;(2)求的最小值.19.(本小题满分12分)如图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.《强化训练练习题(一)第2页》(1)沿图中虚线将它们折叠起来,使P、Q、R、S四点重合,请画出其直观图,试问需要几个这样的几何体才能拼成一个棱长为6的正方体ABCD—A1B1C1D1?(2)在(1)的条件下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E,求平面AB1E与平面ABC所成二面角(锐角)的余弦值.20.(本小题满分12分)已知函数点P1(x1,y1)和P2(x2,y2)是f(x)的图象上的两个动点,且线段P1P2的中点P的坐标为.(1)求证:a是定值;(2)对于任意的正整数n,设试判断数列{Sn}是否为等差数列,若是,请加以证明;若不是,说明理由.21.(本小题满分12分)如图,已知椭圆经过椭圆C的右焦点F且以《强化训练练习题(一)第3页》为方向向量的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆C于N点.(1)证明:(2)求的值.22.(本小题满分14分)已知函数(1)若在上单调递增,求的取值范围;(2)若定义在区间D上的函数对于区间D上的任意两个值总有以下不等式成立,则称函数为区间D上的“凹函数”.试判断当时,是否为“凹函数”,并对你的判断加以证明.攀枝花市第十二中学校高2007级强化训练数学练习题(一)参考答案《强化训练练习题(一)第4页》一、选择题DBADC,CBBCABB二、填空题13.2;14.;15.84;16.三、解答题17.解:(1)记四项指标全部合格的事件为A0,出现一项指示不合格的事件为A1,则∴这批产品不能出厂的概率(2)要四项指标全部检测完毕才能确定该产品能否出厂,说明抽检的前三项指标中必为两项合格,一项不合格,……(10分)设这样的事件为B...