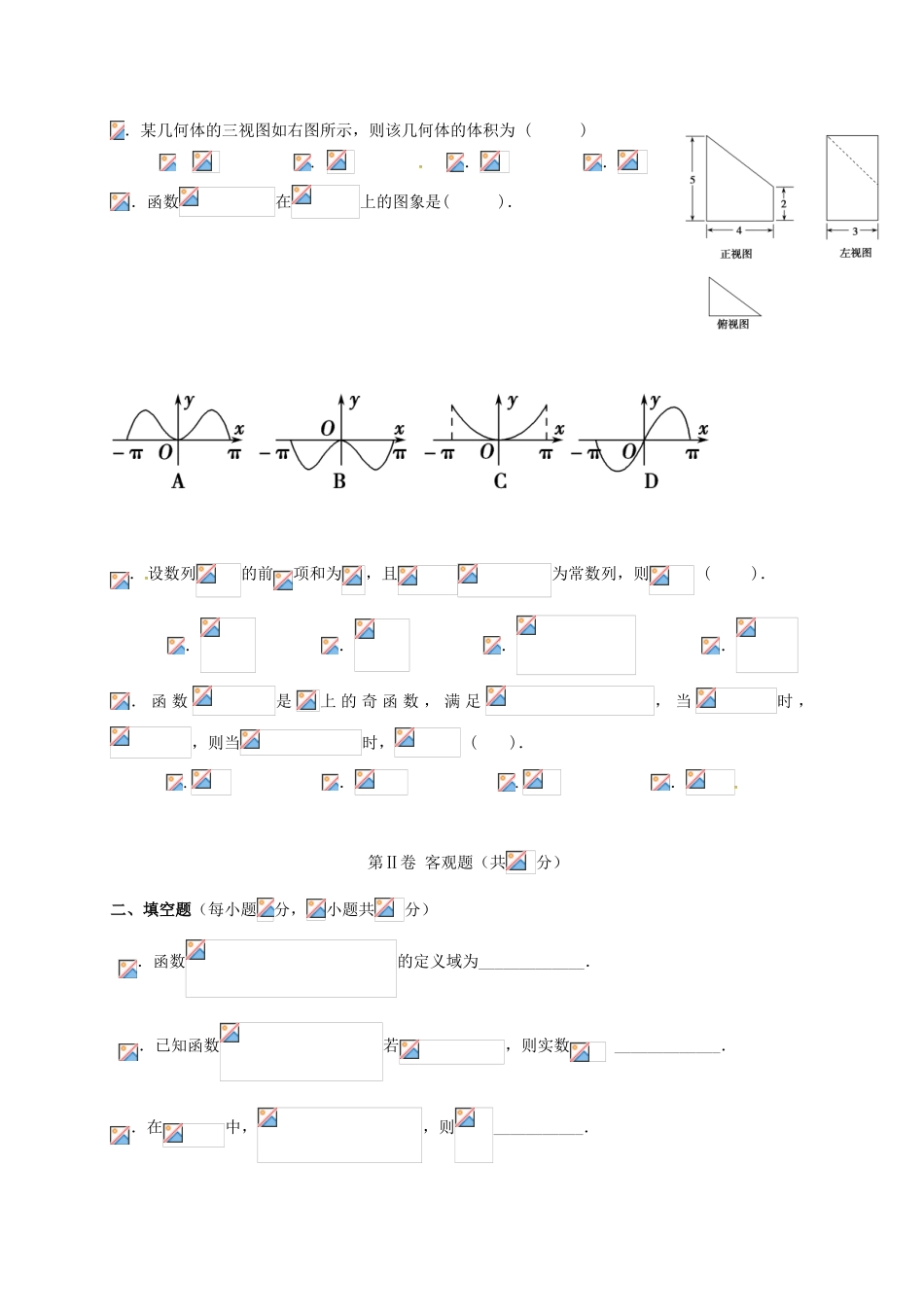
2016—2017学年度下学期阶段测试(三)高一年级数学试卷【考试时间:06月02日】第I卷(选择题,共分)一、选择题:本大题共小题,每小题分。在每小题给出的四个选项中,只有一项是符合题目要求的。.设集合,,则()....如果,那么下列不等式一定成立的是()......在等差数列中,,则()......已知,,,则与的夹角为()......已知是正数,且,则()..有最小值.有最小值.有最大值.有最大值.设是两条不同的直线,是两个不同的平面()..若,则.若,则.若,则.若,则.设,则()......已知,则()...或.或.某几何体的三视图如右图所示,则该几何体的体积为()....函数在上的图象是()..设数列的前项和为,且为常数列,则()......函数是上的奇函数,满足,当时,,则当时,().....第Ⅱ卷客观题(共分)二、填空题(每小题分,小题共分).函数的定义域为_____________..已知函数若,则实数_____________..在中,,则___________..把函数图象上各点的横坐标缩短到原来的(纵坐标不变),再将图象向右平移个单位,那么所得函数解析式为_______________.三、解答题(第题分,其余每题分,共分,解答应写出证明过程或演算步骤).已知集合,.(1)分别求,;(2)已知集合,若,求实数的取值集合..设数列的前项和为,满足(1)求数列的通项公式;(2)设数列的前项和,求.在中,角的对边分别为,且,.(1)求角的大小;(2)若,求边的长和的面积..已知正项等差数列前三项的和等于,并且这三个数分别加上后成为等比数列中的(1)求数列,的通项公式;(2)令,求数列的前项和.如图,四棱锥中,底面为矩形,平面,是的中点.(1)证明:平面;(2)设,三棱锥的体积,求点到平面的距离.PABCDE.已知函数,在同一周期内,当时,取得最大值;当时,取得最小值(1)求函数的解析式;(2)求函数的单调减区间若时,函数有两个零点,求实数的取值范围.2016—2017学年度下学期阶段测试(三)高一数学参考答案一、选择题(每题5分,共60分)1234567891011121.解析:因为集合,则.故选.2.解析:选.3.解析:,故选.4.解析:,解得,因为,所以,故选.5.解析:因为.当且仅当且.即时取等号。故选6.解析:本题可借助特殊图形求解,画一个正方体作为模型(如图).设底面ABCD为α,侧面A1ADD1为β.①当A1B1=m,B1C1=n时,显然A不正确;②当B1C1=m时,显然D不正确;③当B1C1=m时,显然B不正确.故选C.7.解析:,所以,故选.8.解析:因为,所以,所以,解得或。若则所以;若,则,综上,故选.9.解析:此几何体是由一个三棱柱截去一个三棱锥得到的,三棱柱和三棱锥的底面都是直角三角形,两直角边长分别为3和4,其面积为6,三棱柱的高为5,三棱锥的高为3,所以该几何体的体积为6×5-×6×3=24,故选C.10.解析:容易判断函数y=xsinx为偶函数,可排除D.当0<x<时,y=xsinx>0,当x=π时,y=0,可排除B,C,故选A.11.解析:由题意当时,,从而,有,当时上式成立,故选B.12.解析:因为,故直线是函数的一条对称轴,又有函数是上的奇函数,故原点是函数的一个对称中心,则是函数的一个周期,设则,,即,故选.二、填空题(每题5分,共20分)13.解析:由题意解得-3<x≤0故定义域为.14.解析:f(f(0))=f(2)=4+2a=4a,解得a=2.15.解析:,,解得因为,所以,则,所以,故16.解析:将y=sin图象上各点的横坐标缩短到原来的(纵坐标不变),得到函数y=sin;再将图象向右平移个单位,得到函数y=sin=sin.三、解答题(其中第17题10分,其余每题12分,共70分)17.解:(Ⅰ),…………5分(Ⅱ)①当时,,此时;②当时,,则;综合①②,可得的取值范围是………………10分18.解:(1)由题意有,,两式相减得,()又,故数列是首项为,公比为的等比数列,故-----------------6分(2)由(1),所以-----12分19.解:因为,所以,因为所以,所以,,所以……6分因为,所以由余弦定理得,即,解得或(舍)所以………………12分20.(1)设等差数列的公差为,由已知得,则所以中的依次为依题意有解得或(舍去),故,又所以…………6分因为,,所以...