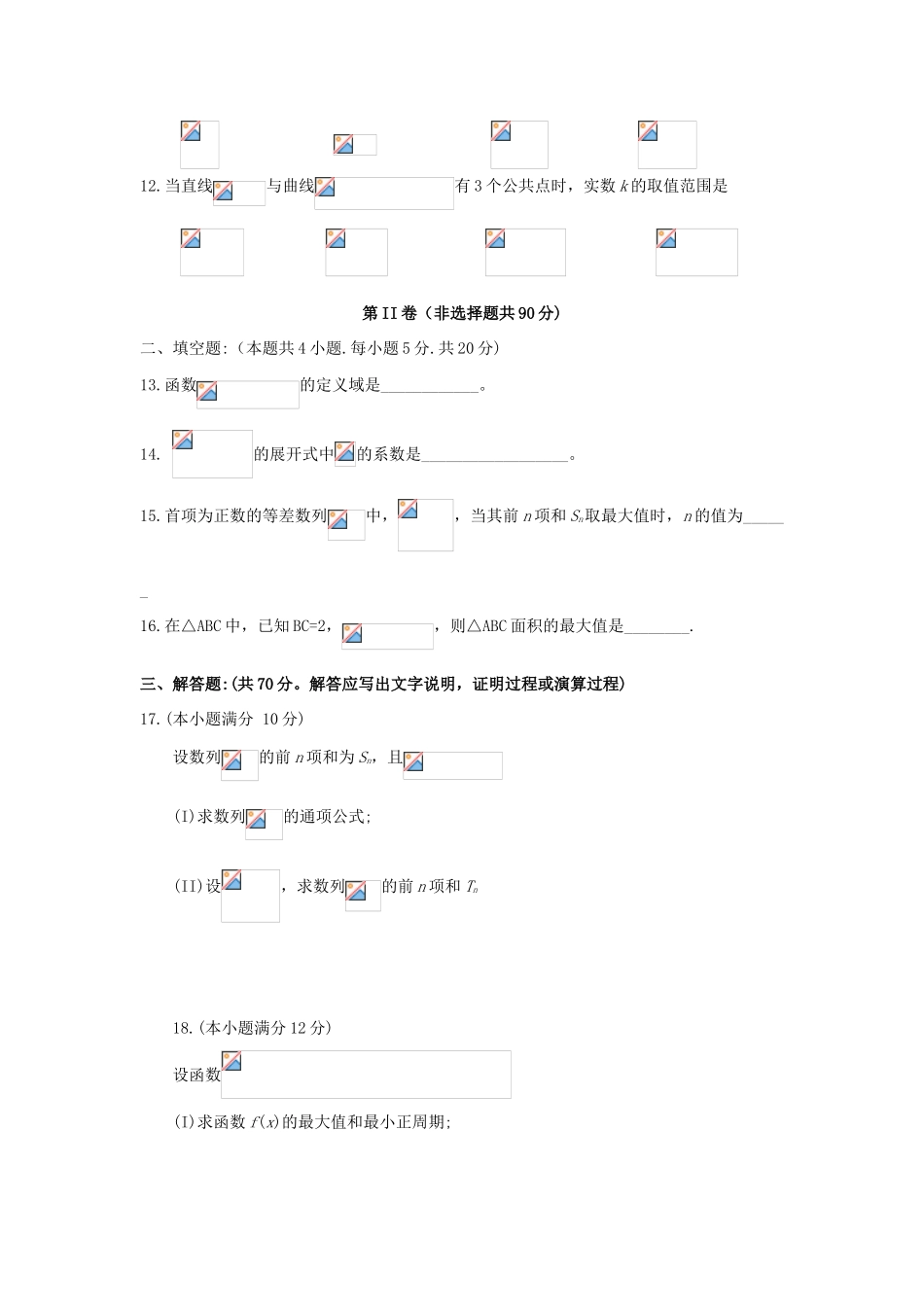
河北省石家庄市2018届高三毕业班9月模拟考试数学(理)试题第I卷(选择题共60分)一、选择题:(共12题.每小题5分.共60分.在每小题给出的四个选项中只有一项是符合题目要求的)1.若集合2.抛物线y=2x2的焦点坐标是3.已知复数:满足(z一2)i=1+i(i为虚数单位),则z的模为A.2B.4C.10D.4.右图是容量为100的样本频率分布直方图,则样本数据在[6,10)内的频数是A32B.8C.24D365.如图,网格纸上小正方形的边长为1,粗线画的是一个几何体的三视图.则该几何体的体积为6.等比数列中,若,且a1,、a2+l、a3成等差数列,则其前5项和为A.30B.32C.62D.647.执行如图所示的程序框图,当输入n为7时,输出S的值是A.14B.210C.42D.840S.已知非零向量、满足,则与的夹角是9.将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个小球,其号码为a,放回后,乙从此口袋中再摸出一个小球,其号码为b,则事件“不等式成立”发生的概率为10.双曲线的左、右焦点分别为F1、F2,过F1作倾斜角为的直线与y轴和双曲线右支分别交于A、B两点,若点A平分F1B,则该双曲线的离心率是11.三梭锥P-ABC中,PC⊥平面ABC,且AB=BC=CA=PC=2,则该三棱锥的外接球的表面积是12.当直线与曲线有3个公共点时,实数k的取值范围是第II卷(非选择题共90分)二、填空题:(本题共4小题.每小题5分.共20分)13.函数的定义域是____________。14.的展开式中的系数是__________________。15.首项为正数的等差数列中,,当其前n项和Sn取最大值时,n的值为______16.在△ABC中,已知BC=2,,则△ABC面积的最大值是________.三、解答题:(共70分。解答应写出文字说明,证明过程或演算过程)17.(本小题满分10分)设数列的前n项和为Sn,且(I)求数列的通项公式;(II)设,求数列的前n项和Tn18.(本小题满分12分)设函数(I)求函数f(x)的最大值和最小正周期;(II)在中,内角A、B、C的对边为a、b、c,若a=2,,且,求b的值19.(本小题满分12分)共享单车的推广给消费者带来全新消费体验,迅速赢得广大消费者的青睐,然而,同时也暴露出管理、停放、服务等方面的问题.为了了解公众对共享单车的态度(“提倡”或“不提倡"),某调研小组随机的对不同年龄段50人进行调查,将调查情况整理如下表:并且,年龄在[20,25)和[40,45)的人中持“提倡”态度的人数分别为5和3.再从这两个年龄段中各随机抽取2人征求意见.(I)求年龄在〔20,25)中被抽到的2人都持“提倡”态度的概率,(II)若抽到的4人中持“不提倡”态度的人数为X.求随机变量X的分布列和数学期望E(X).20.(本小题满分12分)如图,三梭锥P-ABC中,AB⊥AC,且PA=PC=AC=2,PB=BC=(I)求证:平面PAC⊥平面ABC;(Q)求直线PB与平面ABC所成的角.21.(本小题满分12分)已知椭圆与双曲线共焦点,且过点(I)求椭圆的方程;(II)设坐标原点O,过椭圈右焦点的直线l交椭圈于A、B两点,若椭圆上点E与线段AB的中点N满足,求弦长22.(本小题满分12分)已知函数(I)当时,求曲线y=f(x)在x=1处的切线的方程,(II)若a<0,且对任意,都有,求实数a的取值范圈.理科数学9月模拟考试答案一、选择题CCDABCBBCADA二、填空题13.(0,+∞);14.45;15.6;16.错误!未找到引用源。三、解答题17.解:(Ⅰ)由2Sn=3an-1①2Sn-1=3an-1-1②()①-②得2an=3an-3an-1,∴=3,…………………3分又当n=1时,2S1=3a1-1,即a1=1,(符合题意)∴{an}是首项为1,公比为3的等比数列,∴an=3n-1.………………………5分(Ⅱ)由(Ⅰ)得:bn=∴Tn=+++…+,…………………③Tn=++…++,…………④…………………7分③-④得:Tn=+++…+-………………9分=-=-∴Tn=-.……………………………………………10分18.解:(Ⅰ) f(x)=sin(2x-)+cos2x-=sin2x-cos2x+-………………2分=sin2x.……………4分当sin2x=1时,f(x)取得最大值;f(x)的最小正周期是π.………………6分(Ⅱ)f()=sinA=,∴sinA=.………………………………………8分由正弦定理,得:=,∴b=…………………10分==5.…………………12分19.解:(Ⅰ)记年龄在[20,25)中被抽到的2人都持“提倡”态度为事件A.则P(A)=………………………...