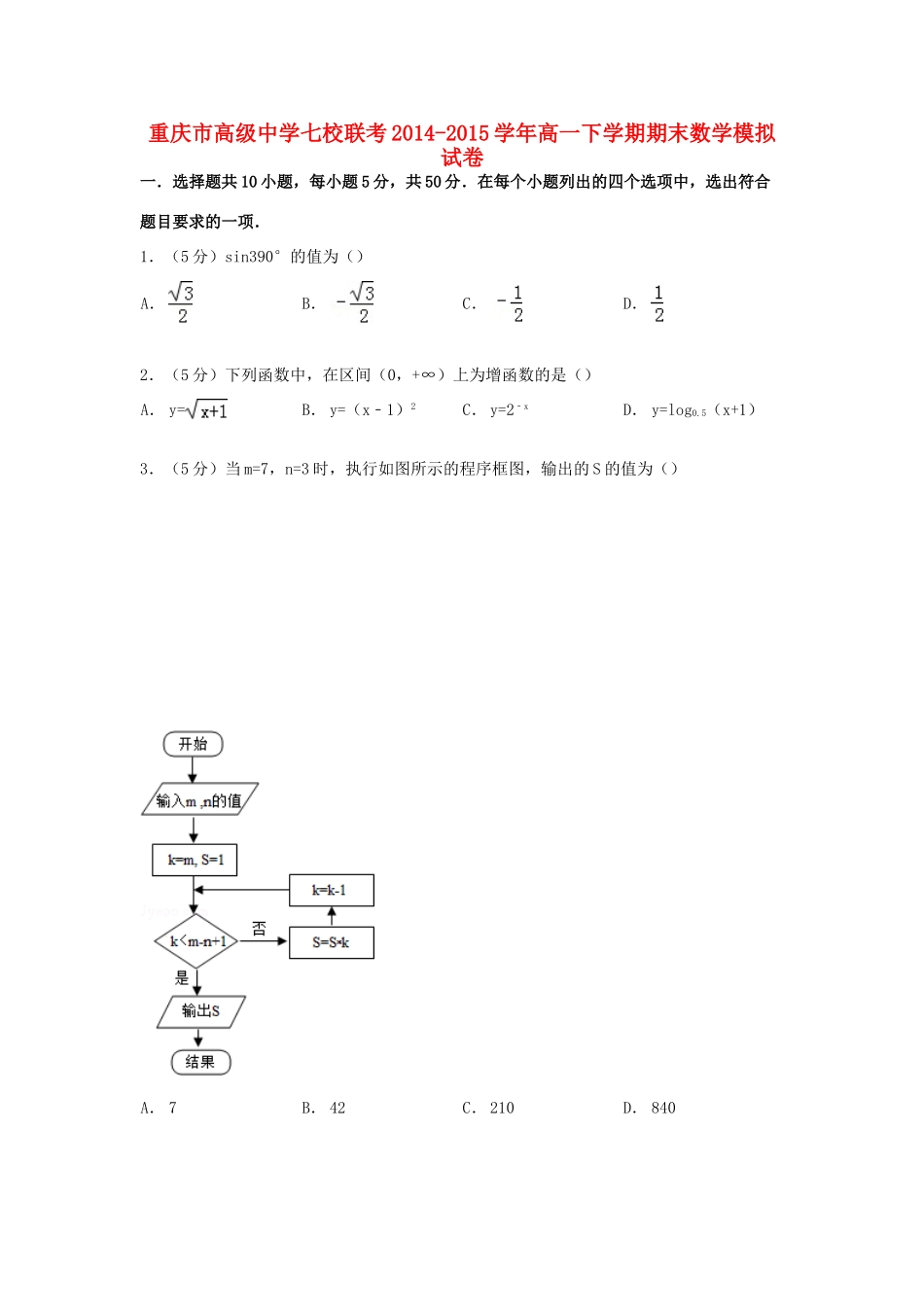
重庆市高级中学七校联考2014-2015学年高一下学期期末数学模拟试卷一.选择题共10小题,每小题5分,共50分.在每个小题列出的四个选项中,选出符合题目要求的一项.1.(5分)sin390°的值为()A.B.C.D.2.(5分)下列函数中,在区间(0,+∞)上为增函数的是()A.y=B.y=(x﹣1)2C.y=2﹣xD.y=log0.5(x+1)3.(5分)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()A.7B.42C.210D.8404.(5分)若x,y满足且z=y﹣x的最小值为﹣4,则k的值为()A.2B.﹣2C.D.﹣5.(5分)在△ABC中,若,则∠B等于()A.30°B.45°C.60°D.90°6.(5分)已知等差数列{an}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=()A.123B.105C.95D.237.(5分)已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列的前100项和为()A.B.C.D.8.(5分)学校餐厅每天供应500名学生用餐,每星期一有A、B两种菜可供选择.调查表明,凡是在这星期一选A菜的,下星期一会有20%改选B菜;而选B菜的,下星期一会有30%改选A菜.用an表示第n个星期一选A的人数,如果a1=428,则a4的值为()A.324B.316C.304D.3029.(5分)已知实数a,b,c满足不等式0<a<b<c<1,且M=2a,N=5﹣b,P=,则M、N、P的大小关系为()A.M>N>PB.P<M<NC.N>P>MD.P>N>M10.(5分)已知平面向量,,满足||=,||=1,•=﹣1,且﹣与﹣的夹角为45°,则||的最大值等于()A.B.2C.D.1二.填空题:本大题共四小题,每小题5分.11.(5分)若集合A={x|x2﹣2x<0},B={x|y=lg(x﹣1)},则A∩B为.12.(5分)设a,b>0,a+b=5,则的最大值为.13.(5分)设△ABC的内角A,B,C的对边分别为a,b,c,且a=2,cosC=﹣,3sinA=2sinB,则c=.14.(5分)在区间[0,5]上随机地选择一个数p,则方程x2+2px+3p﹣2=0有两个负根的概率为.15.(5分)若函数f(x)=|x+1|+2|x﹣a|的最小值为5,则实数a=.三.解答题:本大题共有6小题,共75分.解答应写出相应的过程、证明过程或演算步骤.16.(12分)已知函数f(x)=sin(﹣x)sinx﹣x(Ⅰ)求f(x)的最小正周期和最大值;(Ⅱ)讨论f(x)在上的单调性.17.(12分)随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如下:分组频数频率[25,30]30.12(30,35]50.20(35,40]80.32(40,45]n1f1(45,50]n2f2(1)确定样本频率分布表中n1,n2,f1和f2的值;(2)根据上述频率分布表,画出样本频率分布直方图;(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.18.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.(xi﹣)2(wi﹣)2(xi﹣)(yi﹣)(wi﹣)(yi﹣)46.65636.8289.81.61469108.8表中:=wi(Ⅰ)根据散点图判断,y=a+bx与,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);(Ⅱ)根据(I)的判断结果及表中数据,建立y关于x的回归方程;(Ⅲ)已知这种产品的年利润z与x,y的关系为z=0.2y﹣x,根据(II)的结果回答下列问题:(i)当年宣传费x=49时,年销售量及年利润的预报值时多少?(ii)当年宣传费x为何值时,年利润的预报值最大?并求出最大值19.(13分)已知等差数列{an}满足a3=2,前3项和S3=.(Ⅰ)求{an}的通项公式;(Ⅱ)设等比数列{bn}满足b1=a1,b4=a15,求{bn}前n项和Tn.20.(13分)已知关于x的不等式|x+a|<b的解集为{x|2<x<4}(Ⅰ)求实数a,b的值;(Ⅱ)求+的最大值.21.(13分)已知数列{an}满足a1=1,|an+1﹣an|=pn,n∈N*.(Ⅰ)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;(Ⅱ)若p=,且{a2n﹣1}是递增数列,{a2n}是递减数列...