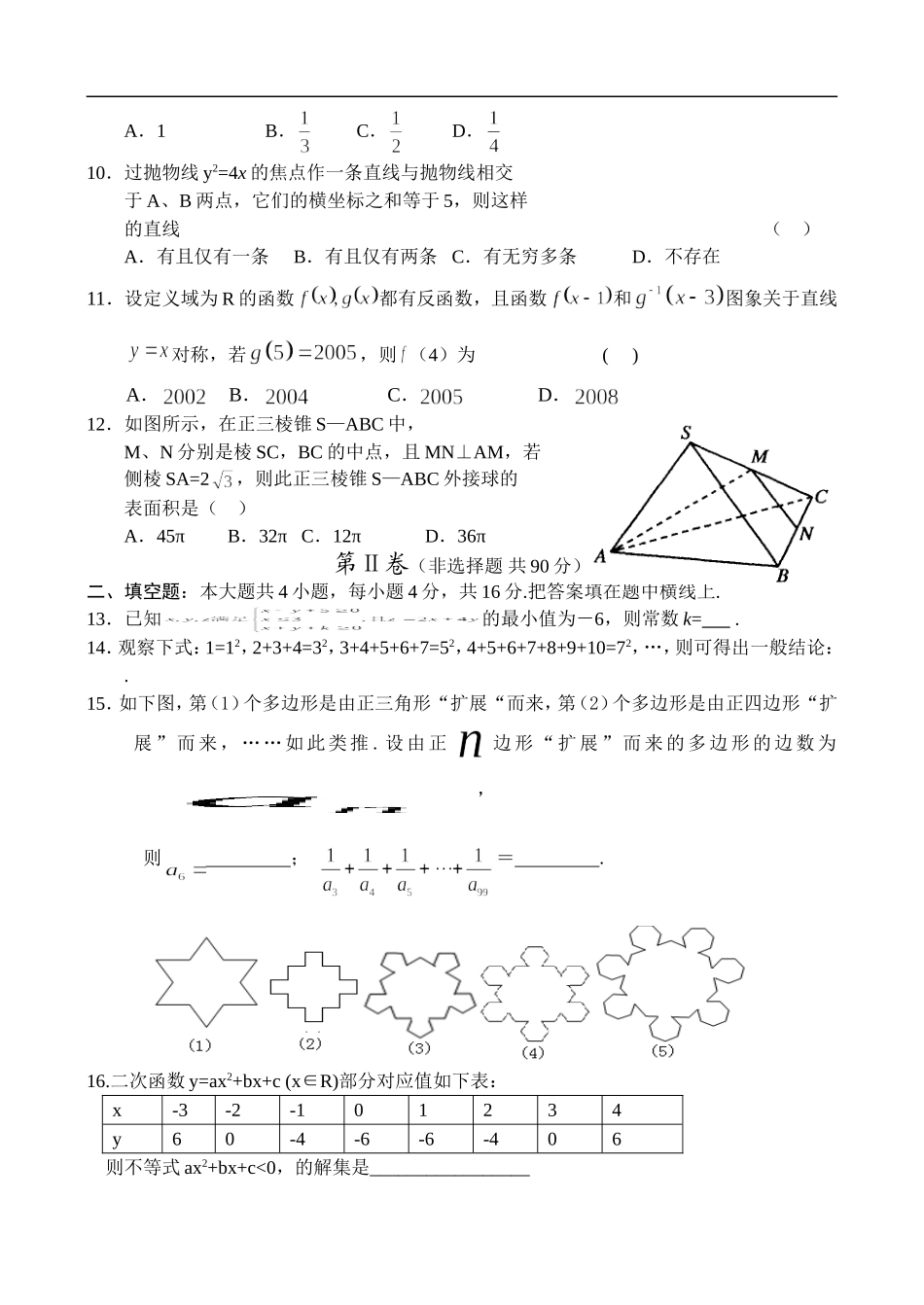
德惠实验中学2009年高三数学第二次双周考(理科)试题第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题;每小题5分,共计60分。在每小题列出的四个选项只有一项是最符合题目要求的。1.复数的虚部是()A.1B.-1C.iD.-i2.已知集合,R是实数集,则(B)∩A=()A.[0,1]B.C.D.以上都不对3.对具有线性相关关系的变量x和y测得一组数据如下:x24568y34657若已求得它们的回归直线的斜率为2,则这条回归的直线议程为()A.y=2x+5B.y=2x-5C.y=4x+5D.y=-2x-54.已知条件p:x≤1,条件,q:<1,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.即非充分也非必要条件5.若函数f(x)=sinax+cosax(a>0)的最小正周期为1,则它的图像的一个对称中心为()A.(-,0)B.(0,0)C.(-,0)D.(,0)6.若的展开式各项系数和为64,则展开式中的常数项为()A.-540B.-162C.162D.5407.身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有()A、48种B、72种C、78种D、84种8.已知函数是定义域为R的偶函数,且,若在上是减函数,那么在上是()A.增函数B.减函数C.先增后减的函数D.先减后增的函数9.已知函数f(x)=2x的反函数f-1(x)满足f-1(a)+f-1(b)=4,则的最小值为()2007A.1B.C.D.10.过抛物线y2=4x的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线()A.有且仅有一条B.有且仅有两条C.有无穷多条D.不存在11.设定义域为R的函数都有反函数,且函数和图象关于直线对称,若,则(4)为()A.B.C.D.12.如图所示,在正三棱锥S—ABC中,M、N分别是棱SC,BC的中点,且MN⊥AM,若侧棱SA=2,则此正三棱锥S—ABC外接球的表面积是()A.45πB.32πC.12πD.36π第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.13.已知的最小值为-6,则常数k=.14.观察下式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…,则可得出一般结论:.15.如下图,第(1)个多边形是由正三角形“扩展“而来,第(2)个多边形是由正四边形“扩展”而来,……如此类推.设由正边形“扩展”而来的多边形的边数为,则;=.16.二次函数y=ax2+bx+c(x∈R)部分对应值如下表:x-3-2-101234y60-4-6-6-406则不等式ax2+bx+c<0,的解集是_________________三、解答题:本大题共6小题,共计74分.解答应写出文字说明、证明过程或推演步骤.17.(本小题满分12分)在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.(Ⅰ)求角B的大小;(Ⅱ)设的最大值是5,求k的值.18.(本题12分)如图,在底面是矩形的四棱锥中,⊥平面,,.是的中点.(Ⅰ)求证:平面⊥平面;(Ⅱ)求二面角所成平面角的余弦值;(Ⅲ)求点到平面的距离.19.(本小题满分12分)某小组有7个同学,其中4个同学从来没有参加过数学研究性学习活动,3个同学曾经参加过数学研究性学习活动.(Ⅰ)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;2007PBEDCA(Ⅱ)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数是一个随机变量,求随机变量的分布列及数学期望E.20.(本小题满分12分)已知定义在R上的单调函数y=f(x),当x<0时,f(x)>1,且对任意的实数x、y∈R,有f(x+y)=f(x)f(y),(Ⅰ)求f(0),并写出适合条件的函数f(x)的一个解析式;(Ⅱ)数列{an}满足,①求通项公式an的表达式;②令,试比较Sn与Tn的大小,并加以证明.21.(本小题满分12分)已知动圆P与定圆B:内切,且动圆P经过一定点A(,0),(Ⅰ)求动圆圆心P的轨迹方程;(Ⅱ)若已知点D(0,3),M、N在动点P的轨迹上,且,求实数的取值范围.22.(本小题满分14分)已知函数和的图象在处的切线互相平行.(Ⅰ)求的值;(Ⅱ)设,当时,恒成立,求的取值范围.参考答案一、选择题(每小题5分,共12小题)BABACABACBCD二、填空题(每小题4分,共4小题)13...