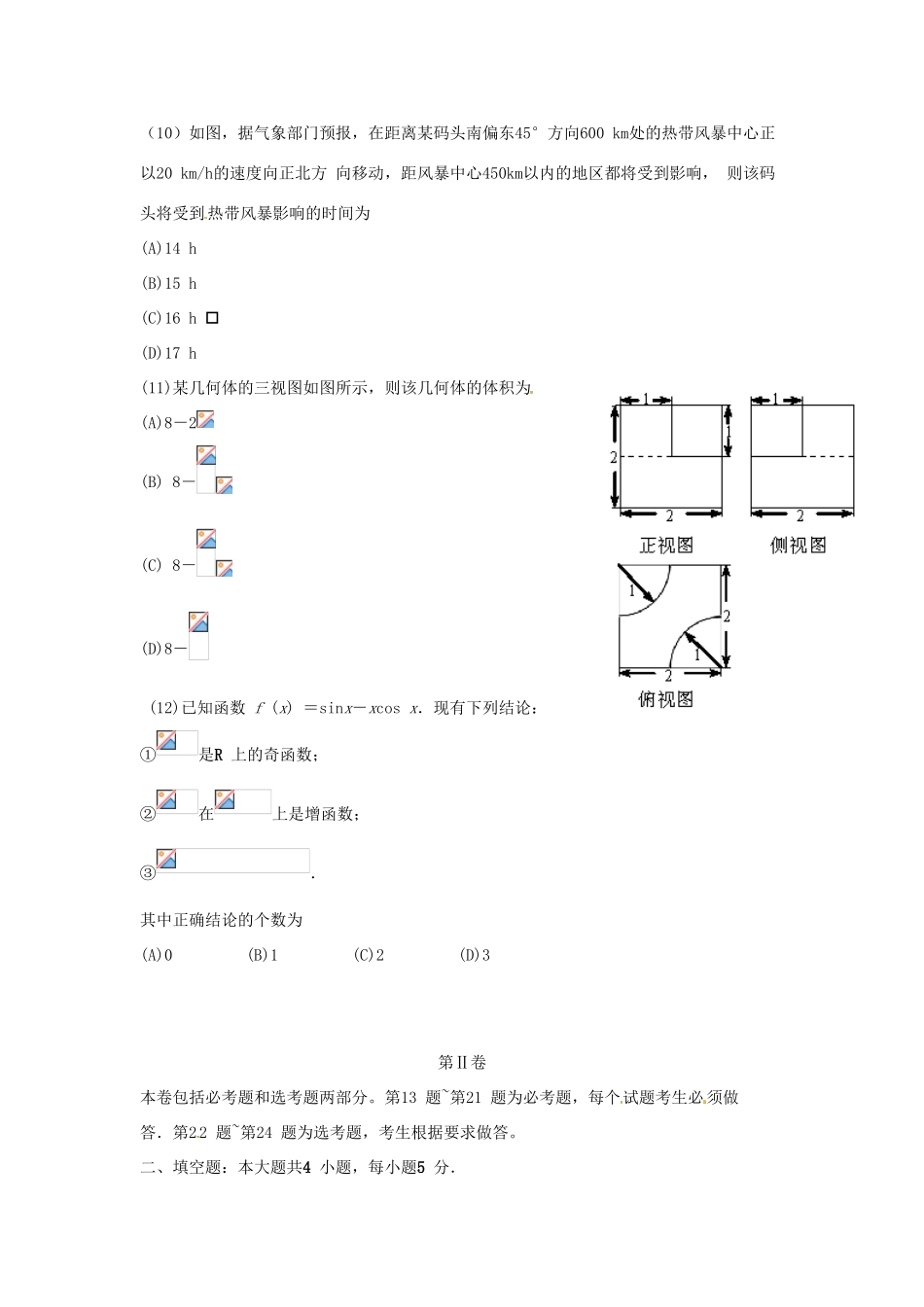
武昌区2016届高三年级元月调研考试文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在本试卷答题卡相应位置上。2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卷上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。4.考试结束后,将本试卷和答题卡一并交回。第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合A={x|},B={x|},则AB(A)(2,3](B)(-,-4)[-2,+)(C)[-2,2)(D)(-,3](4,+)(2)已知(1+2i)=4+3i(其中i是虚数单位,是z的共轭复数),则z的虚部为(A)1(B)-1(C)i(D)-i(3)在区间上随机取一个数x,则事件“”发生的概率为(A)(B)(C)(D)(4)右边程序框图的算法思路源于世界数学名题“3x+1问题”.执行该程序框图,若输入的N=3,则输出i=(A)6(B)7(C)8(D)95)“a≤0”是“函数f(x)=有零点”的(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件(6)已知,且α为第三象限角,则tan2的值等于(A)(B)-(C)(D)-(7)设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内的任意一点,则等于(A)(B)2(C)3(D)4(8)已知抛物线上一点M(,4)到焦点F的距离|MF|=,则直线MF的斜率(A)2(B)(C)(D)(9)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知成等差数列,则cosB的最小值为(A)(B)(C)(D)(10)如图,据气象部门预报,在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动,距风暴中心450km以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为(A)14h(B)15h(C)16h(D)17h(11)某几何体的三视图如图所示,则该几何体的体积为(A)8-2(B)8-(C)8-(D)8-(12)已知函数f(x)=sinx-xcosx.现有下列结论:①是R上的奇函数;②在上是增函数;③.其中正确结论的个数为(A)0(B)1(C)2(D)3第Ⅱ卷本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生必须做答.第22题~第24题为选考题,考生根据要求做答。二、填空题:本大题共4小题,每小题5分.(13)设x,y满足约束条件,则的最小值为.(14)双曲线C:的离心率为,焦点到渐近线的距离为3,则C的实轴长等于.(15)已知,若对任意实数,都有,则实数m的取值范围是(16)已知正四棱锥的顶点都在同一球面上,且该棱锥的高为4,底面边长为2,则该球的表面积为.三、解答题:解答应写出文字说明、证明过程或演算步骤.(17)(本小题满分12分)已知是公差不为0的等差数列{an}的前n项和,S1,S2,S4成等比数列,且,(I)求数列{an}的通项公式;(II)若=,求数列{bn}的前n项和Tn。(18)(本小题满分12分)某城市随机抽取一年内100天的空气质量指数(AQI)的监测数据,结果统计如下:(I)已知某企业每天的经济损失y(单位:元)与空气质量指数x的关系式为若在本年内随机抽取一天,试估计这一天的经济损失超过400元的概率;(II)若本次抽取的样本数据有30天是在供暖季,其中有8天为严重污染.根据提供的统计数据,完成下面的2×2列联表,并判断是否有95%的把握认为“该城市本年的空气严重污染与供暖有关”?(19)(本小题满分12分)在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E,G,F分别为MB,PB,PC的中点,且ADPD2MA.(Ⅰ)求证:平面EFG⊥平面PDC;(Ⅱ)求三棱锥PMAB与四棱锥PABCD的体积之比.(20)(本小题满分12分)过椭圆右焦点F2的直线交椭圆于A,B两点,F1为其左焦点.当直线AB⊥x轴时,△AF1B为正三角形,且其周长为.(Ⅰ)求椭圆的方程;(Ⅱ)设C为直线x=2上的一点,且满足CF2⊥AB,若(其中O为坐标原点),求四边形OACB的面积.(21)(本小题满分12分)已知函数.(Ⅰ)若=0,求的最大值;(Ⅱ)若曲线在点处的切线与直线垂直,证明:请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.做答时请写清...