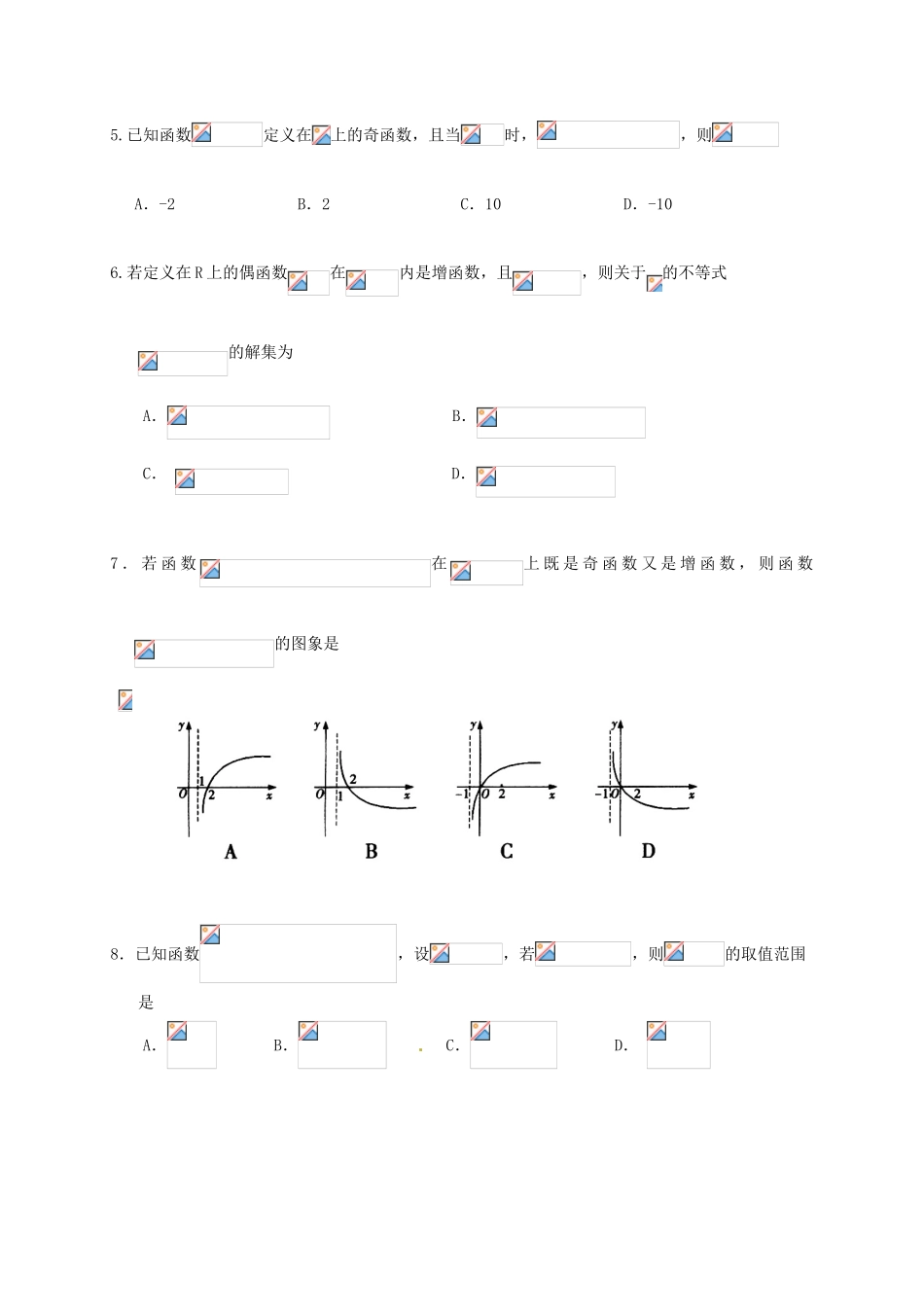
2016学年第一学期期中考试高一数学试题卷本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间为120分钟.第Ⅰ卷(选择题共40分)注意事项:用钢笔将题目做在答题卷上,做在试题卷上无效.一、选择题(每小题5分,共40分)1.设集合,,则下列关系中正确的是A.B.C.D.2.函数且的定义域为A.B.C.D.3.与角终边相同的角是A.B.C.D.4.当时,幂函数的图象不可能经过A.第二、四象限B.第二象限C.第三象限D.第四象限5.已知函数定义在上的奇函数,且当时,,则A.-2B.2C.10D.-106.若定义在R上的偶函数在内是增函数,且,则关于的不等式的解集为A.B.C.D.7.若函数在上既是奇函数又是增函数,则函数的图象是8.已知函数,设,若,则的取值范围是A.B.C.D.第Ⅱ卷(非选择题共110分)注意事项:用钢笔将题目做在答题卷上,做在试题卷上无效.二、填空题:(本大题共7小题,第9-12题每小题6分,第13-15题每小题4分,共36分)9.若角的终边上有一点,则▲,▲.10.已知函数为偶函数,若,则▲,▲.11.计算:▲,▲.12.已知是△ABC的一个内角,,则▲,▲.13.若函数的图象经过定点,则的值是▲.14.直线与函数的图象有四个不同交点,则实数的取值范围是▲.15.已知函数若对任意,恒有,则的取值范围是▲.三、解答题:(本大题共5小题,共74分)16.(本题14分)集合.(Ⅰ)求;(Ⅱ)求;(Ⅲ)若,求实数的取值范围.17.(本题15分)已知二次函数,当时恒成立,且是的一个零点.(Ⅰ)求函数的解析式;(Ⅱ)设,若函数在区间上的最大值等于,求实数的值.18.(本题15分)已知函数.(Ⅰ)若函数的定义域为,求实数的值;(Ⅱ)若且在上为增函数,求实数的取值范围.19.(本题15分)已知,其中.(Ⅰ)若对任意,恒有求实数的值;(Ⅱ)若,求的最小值.20.(本题15分)已知定义在区间上的函数,其中常数.(Ⅰ)若函数分别在区间上单调,试求实数的取值范围;(Ⅱ)当时,方程有四个不相等的实根.①求四根之积的值;②在上是否存在实数,使得在上单调且取值范围为?若存在,求出的取值范围;若不存在,请说明理由.2016学年第一学期期中考试高一数学参考答案一.DACD,BBCA二、9.;10.;11.;12.;13.2;14.;15.三、16.(本题14分)集合.(Ⅰ)求;(Ⅱ)求;(Ⅲ)若,求实数的取值范围.解:(Ⅰ)=……………………………………………………………………4分(Ⅱ),………………………………10分(Ⅲ),……………………………………………………………………14分17.(本题15分)已知二次函数,当时恒成立,且是的一个零点.(Ⅰ)求函数的解析式;(Ⅱ)设,若函数在区间上的最大值等于,求实数的值.解:(Ⅰ)由时恒成立得,也即恒成立,………………………………………3分又是的一个零点,.……………………………………………6分…………………………………………………………………………………7分(Ⅱ)设,…………………………………………9分若,则由得,此时,符合题意;……………12分若,则可得不合题意……………………………………………………………………………………………15分18.(本题15分)已知函数.(Ⅰ)若函数的定义域为,求实数的值;(Ⅱ)若且在上为增函数,求实数的取值范围.解:(Ⅰ)由题意,不等式的解集是,所以是方程的两实根,,即……………………………………………………………………………………7分(Ⅱ)设,由得,………………………10分又在上为增函数,所以在上是减函数且恒为正数,也即得.…………………15分19.(本题15分)已知,其中.(Ⅰ)若对任意,恒有求实数的值;(Ⅱ)若,求的最小值.解:(Ⅰ)对任意,时,恒成立,………………………………………3分即恒成立……………………………………6分(Ⅱ)若,则也即所以上面不等式的解是…………………………………………9分(1)当,即时,在递减,在递增,所以的最小值………………………………12分(2)当,即时,在递减,在递增的最小值所以………………………………………………15分20.(本题15分)已知定义在区间上的函数,其中常数.(Ⅰ)若函数分别在区间上单调,试求实数的取值范围;(Ⅱ)当时,方程有四个不相等的实根.①求四根之积...