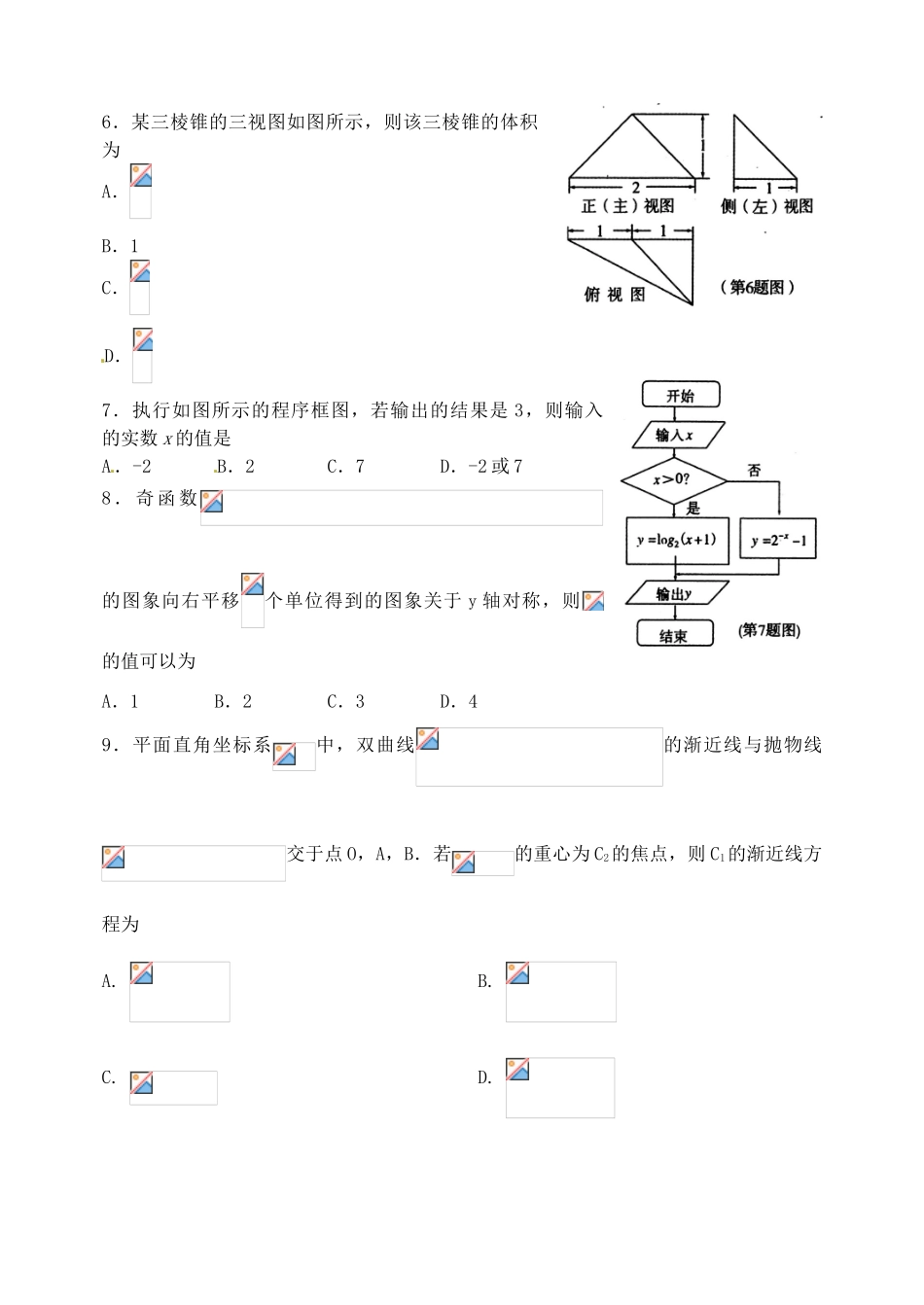
2016年济宁市高考模拟考试高三数学(理)试题2016.05本试卷分第I卷(选择题)和第II卷(非选择题)两部分.满分150分.考试时间120分钟.考试结束后,将本试卷和答题卡一并收回.注意事项:1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上.第I卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,则A.(0,1]B.C.(1,2)D.[1,2)2.设i是虚数单位,在复平面内复数的共轭复数对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.由曲线,直线所围成的封闭图形的面积是A.B.C.D.14.若的二项展开式中含项的系数是36,则实数A.1B.-1C.D.45.有下列三个说法:①命题“”的否定是“”;②“为真”是“为假”的必要不充分条件;③在区间上随机取一个数戈,则事件“”发生的概率为.其中正确说法的个数是A.0B.1C.2D.36.某三棱锥的三视图如图所示,则该三棱锥的体积为A.B.1C.D.7.执行如图所示的程序框图,若输出的结果是3,则输入的实数x的值是A.-2B.2C.7D.-2或78.奇函数的图象向右平移个单位得到的图象关于y轴对称,则的值可以为A.1B.2C.3D.49.平面直角坐标系中,双曲线的渐近线与抛物线交于点O,A,B.若的重心为C2的焦点,则C1的渐近线方程为A.B.C.D.10.已知函数是定义在R上的偶函数,当时,,若函数恰有4个不同的零点,则实数k的取值范围是A.]B.C.D.第Ⅱ卷(非选择题共100分)注意事项:1.第Ⅱ卷共2页,必须使用0.5毫米的黑色墨水签字笔书写,要字体工整,笔迹清晰,严格在题号所指示的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共5小题,每小题5分,共25分.11.一个总体中有80个个体,随机编号为0,1,2,…,79,依编号顺序平均分成8个小组,组号依次为1,2,3,…,8.现用系统抽样方法抽取一个容量为8的样本,若在第l组随机抽取的号码为5,则在第6组中抽取的号码是▲.12.设变量满足约束条件则目标函数的最小值为▲.13.已知向量,其中,且,则▲.14.不等式的解集为▲.15.若函数上单调递减,则实数a的取值范围是▲..三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知函数.(I)当时,求函数的值域;(II)在中,内角A,B,C的对边分别为,若且sinB=2sinC,求的面积.17.(本小题满分12分)某校高二年级开设五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选a课程,不选b课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.(I)求甲同学选中c课程且乙同学未选中c课程的概率;(II)用X表示甲、乙、丙选中c课程的人数之和,求X的分布列和数学期望.18.(本小题满分12分)如图,在四棱锥A—BCDE中,,垂足为F,BE平面ABC,CD∥BE,BC=4,BE=3,CD=1.(I)证明:EFAD;(II)求平面ADE与平面ADF所成的锐二面角的余弦值.19.(本小题满分12分)已知数列的前n项和为,在等比数列中,.(I)求数列和的通项公式;(Ⅱ)令,设数列的前n项和为,求.20.(本小题满分13分)已知函数(I)求在上的最小值;(II)若m为整数,当时,恒成立.求m的最大值.21.(本小题满分14分)已知椭圆的离心率为,过椭圆C的左焦点且倾斜角为60°的直线与圆相交,所得弦的长度为.(I)求椭圆C的方程;(II)设椭圆C的上顶点为M,若直线与椭圆C交于两点A,B(A,B都不是上顶点),且直线MA与MB的斜率之积为.(i)求证:直线l过定点;(ii)求△MAB面积的最大值.