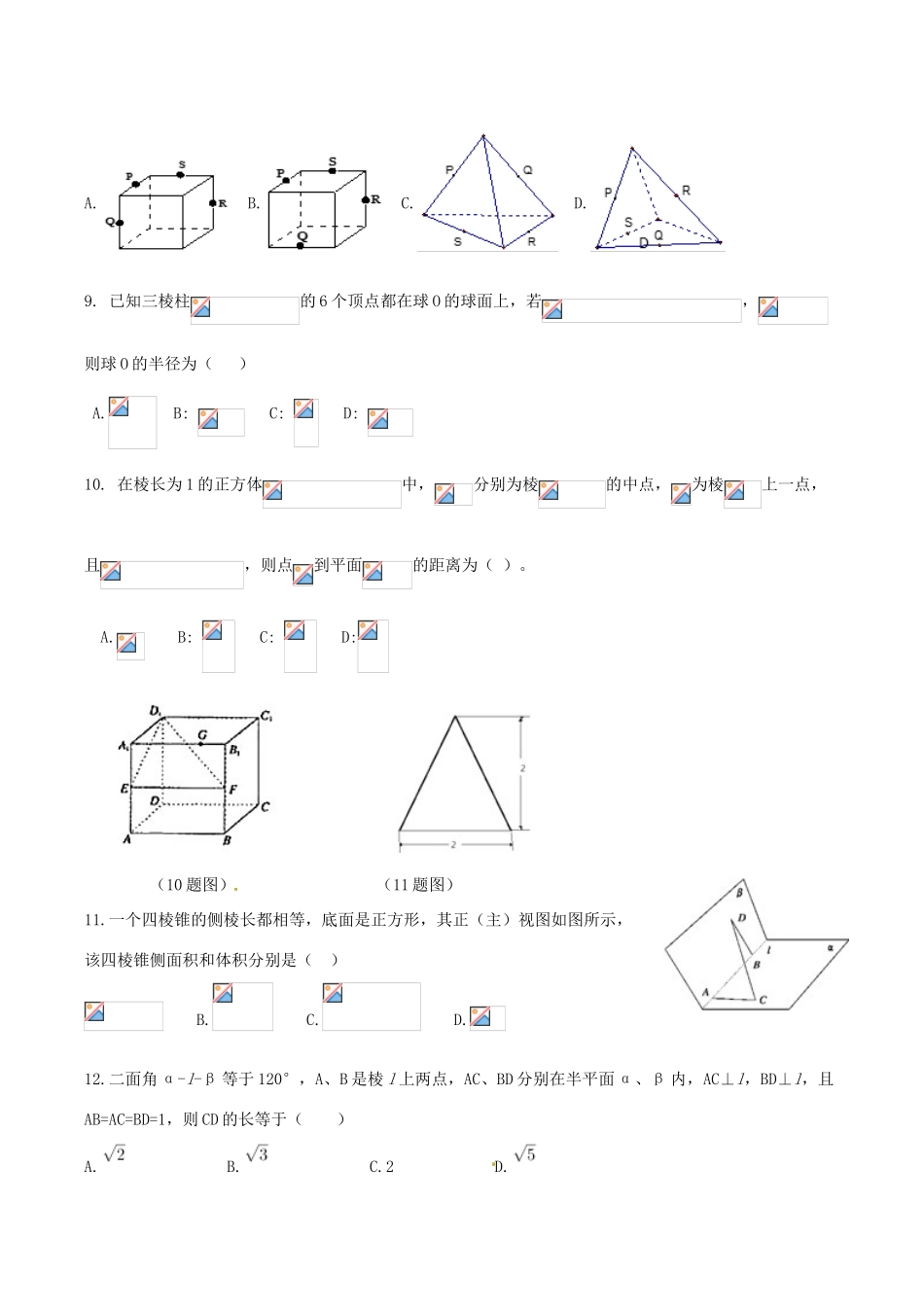
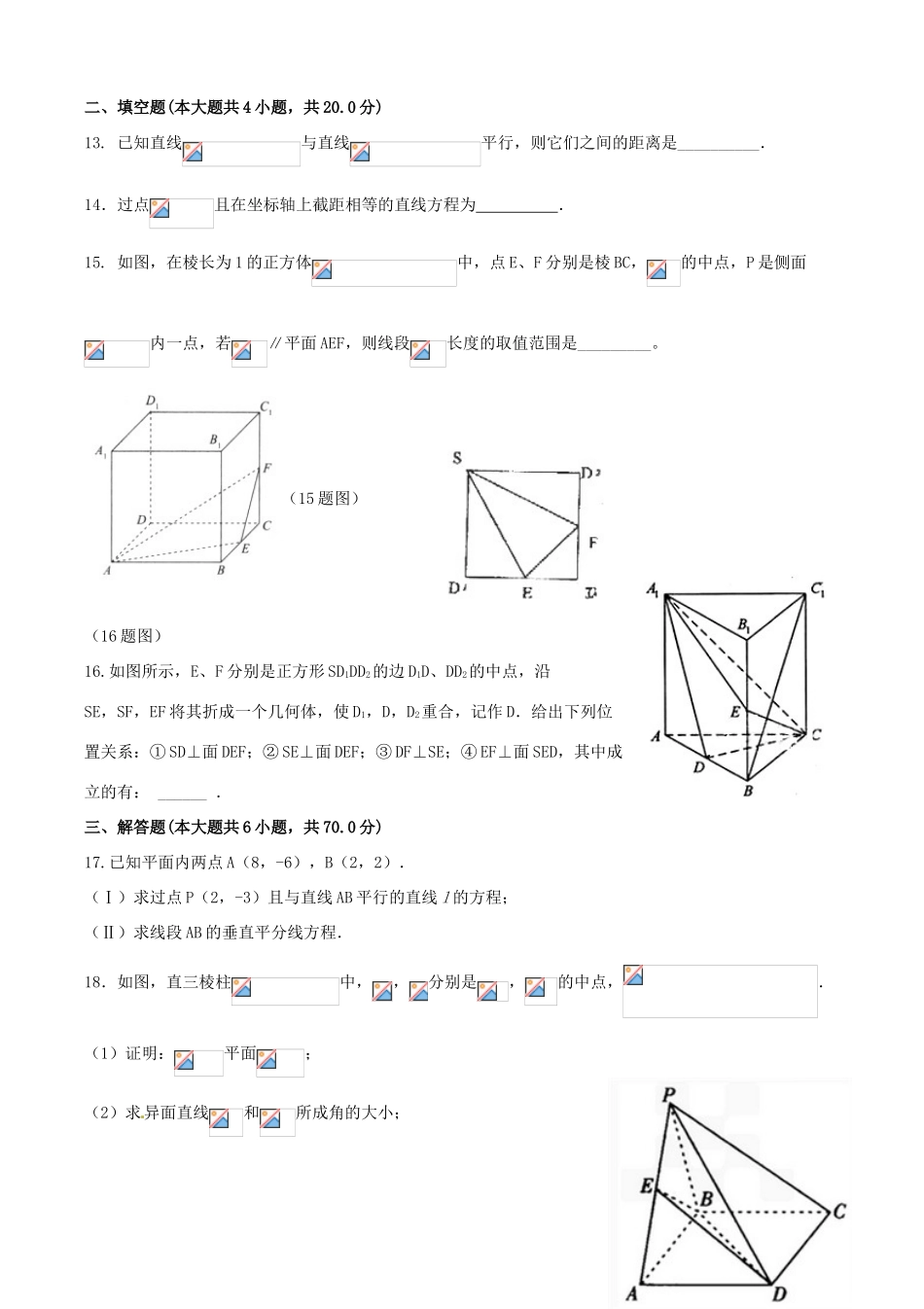
河北省张家口市2016-2017学年高一数学3月月考试题(衔接班)一、选择题(本大题共12小题,共60.0分)1.已知直线方程,则这条直线的倾斜角是()A.150°B.120°C.60°D.30°2.设l,m表示不同直线,α,β表示不同平面,则下列结论中正确的是()A.若l∥α,l⊥m,则m⊥αB.若l∥α,l⊥m,mβ⊂,则α⊥βC.若l∥α,l∥m,则m∥αD.若α∥β,l∥α,l∥m,mβ⊄,则m∥β3.设P是△ABC所在平面α外一点,且P到AB、BC、CA的距离相等,P在α内的射影P′在△ABC内部,则P′为△ABC的()A.重心B.垂心C.内心D.外心4.已知直线l1:ax+2y-1=0,直线l2:8x+ay+2-a=0,若l1∥l2,则实数a的值为()A.±4B.-4C.4D.±25.一个几何体的三视图如图所示,则该几何体的体积为()A.4π+1B.C.D.4π+8(5题图)(6题图)6.如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是()A.30°B.45°C.60°D.90°7.已知A(-2,-1),B(2,-3),过点P(1,5)的直线l与线段AB有交点,则l的斜率的范围是()A.(-∞,-8]B.[2,+∞)C.(-∞,-8]∪[2,+∞)D.8.下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是()A.B.C.D.9.已知三棱柱的6个顶点都在球O的球面上,若,则球O的半径为()A.B:C:D:10.在棱长为1的正方体中,分别为棱的中点,为棱上一点,且,则点到平面的距离为()。A.B:C:D:(10题图)(11题图)11.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,该四棱锥侧面积和体积分别是()B.C.D.12.二面角α-l-β等于120°,A、B是棱l上两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=BD=1,则CD的长等于()A.B.C.2D.二、填空题(本大题共4小题,共20.0分)13.已知直线与直线平行,则它们之间的距离是__________.14.过点且在坐标轴上截距相等的直线方程为.15.如图,在棱长为1的正方体中,点E、F分别是棱BC,的中点,P是侧面内一点,若∥平面AEF,则线段长度的取值范围是_________。(15题图)(16题图)16.如图所示,E、F分别是正方形SD1DD2的边D1D、DD2的中点,沿SE,SF,EF将其折成一个几何体,使D1,D,D2重合,记作D.给出下列位置关系:①SD⊥面DEF;②SE⊥面DEF;③DF⊥SE;④EF⊥面SED,其中成立的有:______.三、解答题(本大题共6小题,共70.0分)17.已知平面内两点A(8,-6),B(2,2).(Ⅰ)求过点P(2,-3)且与直线AB平行的直线l的方程;(Ⅱ)求线段AB的垂直平分线方程.18.如图,直三棱柱中,,分别是,的中点,.(1)证明:平面;(2)求异面直线和所成角的大小;19.如图,四棱锥的底面是矩形,平面平面,是的中点,且,.(Ⅰ)求证:平面;(Ⅱ)求三棱锥的体积.20.如图,三棱柱中,侧棱⊥底面,且各棱长均相等。分别为棱的中点。(1)证明(平行)平面;(2)证明平面⊥平面;(3)求直线与平面所成角的正弦值。<理科>21.如图,是圆的直径,垂直于圆所在的平面,是圆上的点.(1)求证:平面平面;(2)若,求二面角的余弦值.<文科>21.如图,直三棱柱的底面是边长为2的正三角形,分别是的中点.(1)证明:平面⊥平面;(2)若直线与平面所成的角为45°,求三棱锥的体积.22.如图,在长方体中,,点E在棱AB上移动.(1)证明:;(2)当E为AB的中点时,求点E到面的距离;(3)AE等于何值时,二面角的大小为.(理科全做,文科做前两问)答案和解析【答案】1.C2.D3.C4.B5.C6.C7.C8.D9.C10.D11.B12.C13.214.或15.16.①与③17.解:(Ⅰ)因为,所以由点斜式得直线l的方程4x+3y+1=0(Ⅱ)因为AB的中点坐标为(5,-2),AB的垂直平分线斜率为所以由点斜式得AB的中垂线方程为3x-4y-23=018.1.(1)证明见解析;(2).试题解析:(1)证明:连接与相交于点,连接.由矩形可得点是的中点,又是的中点,,平面,平面,平面(2) ,不失一般性令,,∴.以为坐标原点,的方向为轴正方向,的方向为轴正方向,的方向为轴正方向,建立空间直角坐标系.则,,,,,.设异面直线与所成角为,则,∴,∴异面直线与所成角为.考点:线面平行的判定;异面直线所成的角.【一题多...