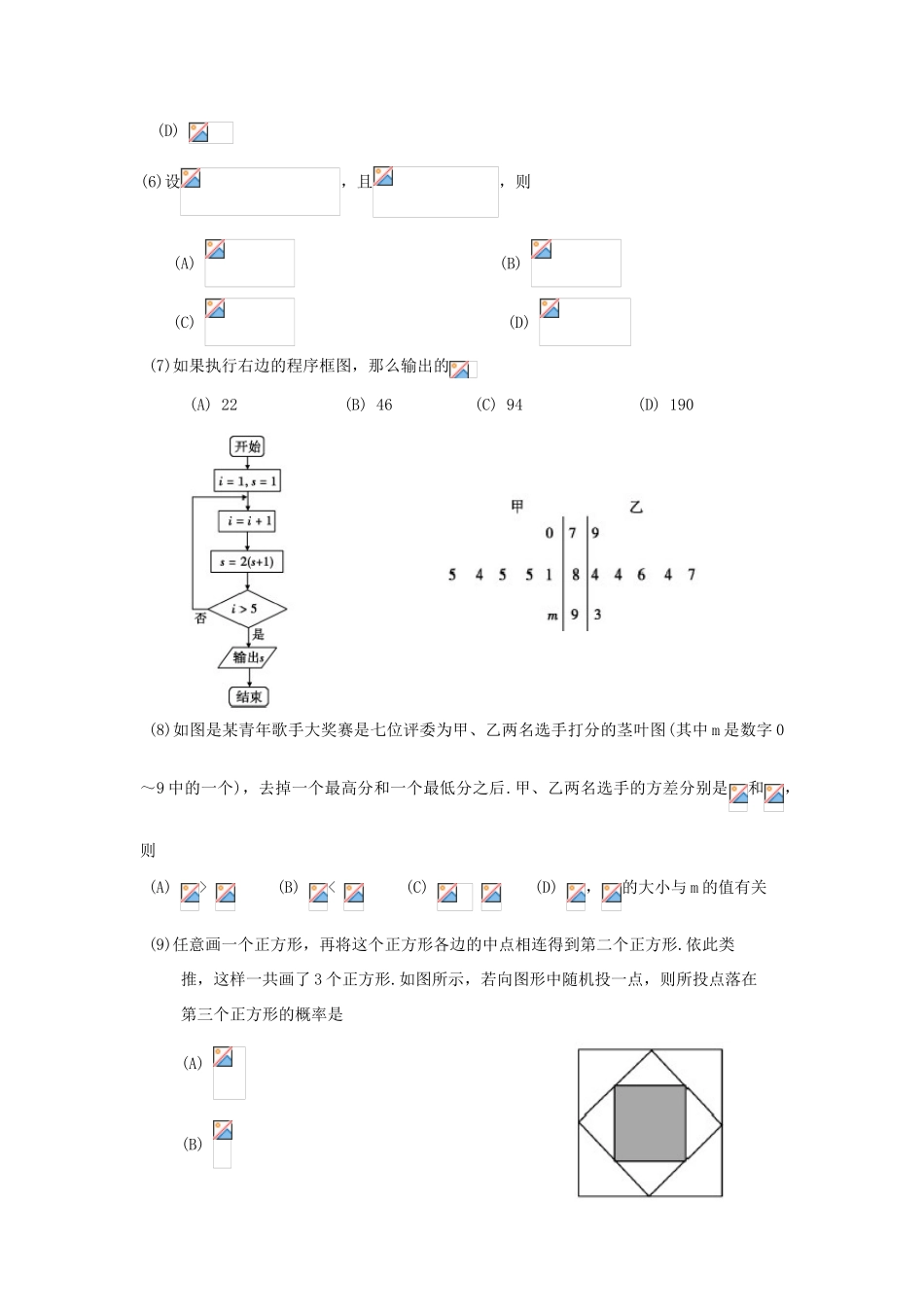
2016-2017学年度第二学期期末考试高一数学注意事项:1.本试卷备有答题卡,请在答题卡上作答.否则无效。2.本试卷分为第I卷(选择题)和第II卷(非选择题)两部分。考试时间:120分钟.试卷满分:150分。参考公式:回归直线的方程:第I卷(选择题.共60分)一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.(1)己知,那么角是(A)第一或第二象限角(B)第二或第三象限角(C)第三或第四象限角(D)第一或第四象限角(2)从编号为1~50的50枚最新研制的某种型号的弹道导弹中随机抽取5枚来进行发射试验,若采用每部分选取的号码间隔一样的系统抽样方法,则所选取的5枚导弹的编号可能是(A)3、13、23、33、43(B)5、10、15、20、25(C)1、2、3、4、5(D)2、4、8、16、32(3)已知扇形的周长为8cm.则该扇形的面积S值最大时圆心角的大小为(A)4弧度(B)3弧度(C)2弧度(D)1弧度(4)已知:、是不共线向量,,,且,则的值为(A)8(B)3(C)-3(D)-8(5)如果右边程序运行后输出的结果是132.那么在程序中while后面的表达式应为(A)>11(B)(C)(D)(6)设,且,则(A)(B)(C)(D)(7)如果执行右边的程序框图,那么输出的(A)22(B)46(C)94(D)190(8)如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后.甲、乙两名选手的方差分别是和,则(A)>(B)<(C)(D),的大小与m的值有关(9)任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形.依此类推,这样一共画了3个正方形.如图所示,若向图形中随机投一点,则所投点落在第三个正方形的概率是(A)(B)(C)(D)(10)由函数的图象得到的图象,需要将的图象(A)向左平移个单位(B)向右平移个单位(C)向左平移个单位(D)向右平移个单位(11)已知为奇函数,则的一个取值为(A)0(B)(C)(D)(12)函数的图象与直线有且仅有两个不同的交点,则的取值范围是(A)(B)(C)(D)[1.3]第II卷(非选择题,共90分)二、填空题:本大题共4小题.每小题5分,共20分.(13)利用更相减损之术求1230与411的最大公约数时,第三次做差所得差值为________。(14)已知函数的部分图象如图所示.则的解析式是______________。(15)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销.得到如下数据:根据上表可得回归直线方程中的,据此模型预报单价为10元时的销量为_______件.(16)给出下列命题:①函数的最小正周期是②终边在轴上的角的集合是③函数的一个对称中心为④设是锐角三角形。则点在第四象限,其中正确命题的序号是_______________________(把正确命题的序号都填上).三、解答题:本大题共6小题.共70分.解答题应写出文字说明,证明过程和演算步骤.(17)(本题满分12分)己知·(1)求的值(2)若是钝角,是锐角,且,求的值·(18)(本小题满分12分)一个体育训练小组测试的50m跑的成绩(单位:)如下:6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,请设计一个算法,从这些成绩中搜索出小于6.8的成绩.并画出程序框图.(19)(本小题满分12分)为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后.画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(I)第二小组的频率是多少?样本容量是多少?(Il)若次数在110以上(含110次)为达标.试估计该学校全体高一学生的达标率是多少?(III)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.(20)(本小题满分12分)已知向量(I)当时,求的值;(II)当时,求向量与的夹角的余弦值;(III)当时,求(21)(本小题满分12分)M科技公司从45名男员工、30名女员工中按照分层抽样的方法组建了一个5人的科研小组.(I)求某员工被抽到的概率及科研小组中男、女员工的人数;(Il)这个科研小组决定选出两名员工做某项实验,方法是先从小组里选出1名员工做实验,该员工做完后,再从小组内剩下的员工中选一名员工做实验.求选出的两名员工中恰有一名女员工的概率.(22)(本小题满分10分)设向量.(I)若,求的值;(II)设函数,求的最大值及的单调递增区间.