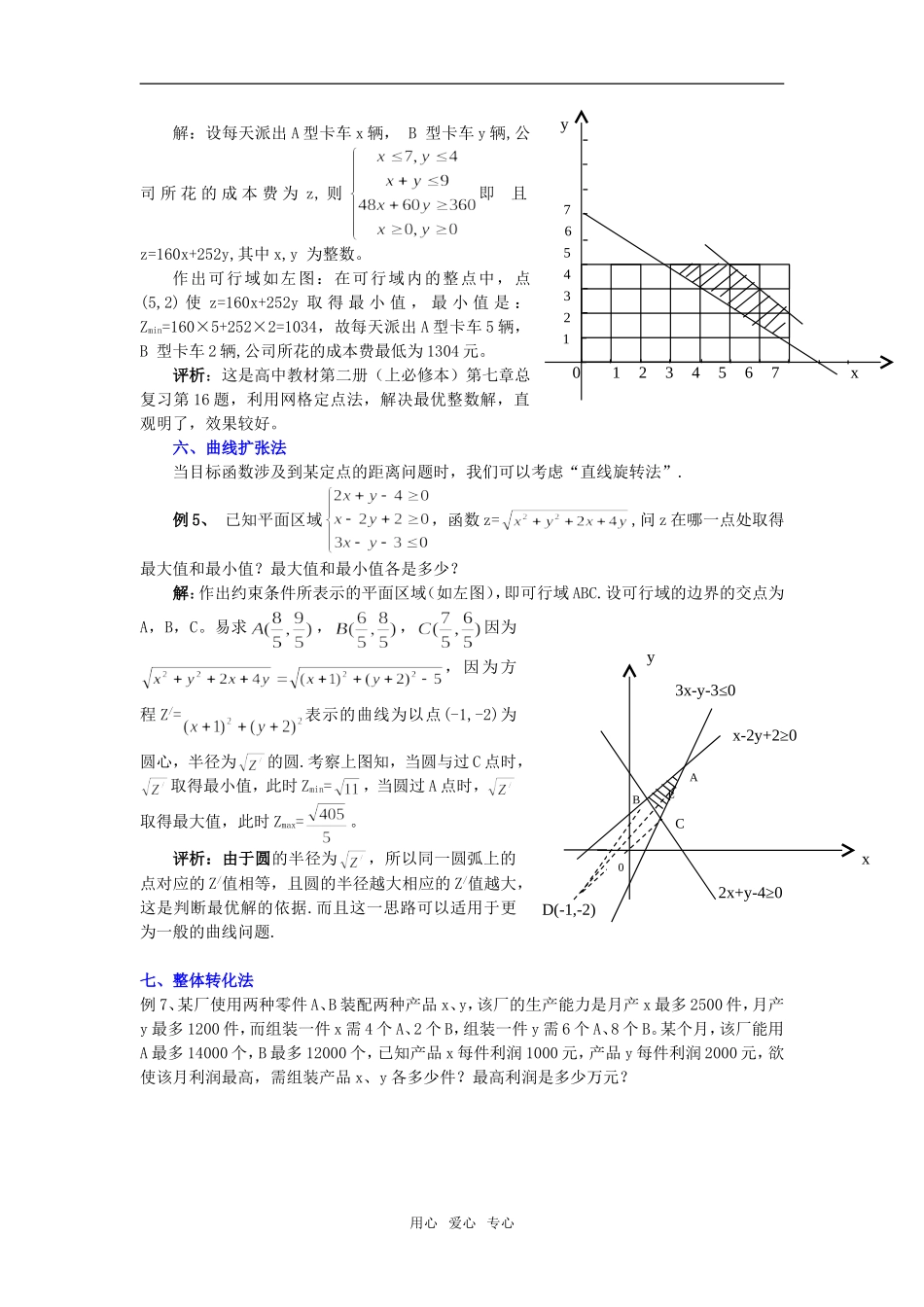
线性目标函数最优解的求解方法线性规划中寻求最优解是解析几何的重点,也是难点。现就如何利用可行域寻求最优解的常见方法作些探讨.一、平移直线法平移法是一种最基本的方法,其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等.例1变量x、y满足下列条件:则使z=3x+2y的值最小的(x,y)是()A.(4.5,3)B.(3,6)C.(9,2)D.(6,4)解析:作出约束条件的可行域(如图),由z=3x+2y知,于是作一系列与直线平行的直线,当直线过图中的B点时,取得最小值。于是由,从而知当时,z=3x+2y取得最小值。故选B。评析:解决线性规划中的最值问题的关键是:作出可行域,找出最优解。二、代入检验法通过平移法可以发现,取得最优解对应的点往往是可行域的顶点,其实这具有必然性.于是在有关选择题的线性规划中的最值问题,可采用求解方程组代入检验的方法求解。例2,已知x、y满足约束条件:,则Z=10x+15y的最大值为()A195B200C210D220解:解程组从而代入Z=10x+15y可得Zmax=195,故选A。评析:代入检验法在涉及最优解为近似解或整格解的问题时,是一种行之有效的方法,具有其它方法不可替代的作用.三、比较斜率法平移法的缺陷在于,当可行域的顶点数较多时,不易直观地判断出哪个或哪几个顶点的坐标是最优解.这时若进一步考虑直线斜率的大小,则可以确定出最优解.例3某工厂生产甲、乙两种产品.已知生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t.甲、乙两种产品应各生产多少(精确到用心爱心专心3692yxCBA122yx2432yxo481216481218xy0.1t),能使利润总额达到最大?解:设生产甲、乙两种产品分别为xt、yt,利润总额为z元,那么且Z=600x+1000y作出约束条件所表示的平面区域(如左图),即可行域.作直线l:600x+1000y=0,即直线l:3x+5y=0.因为,即kEN