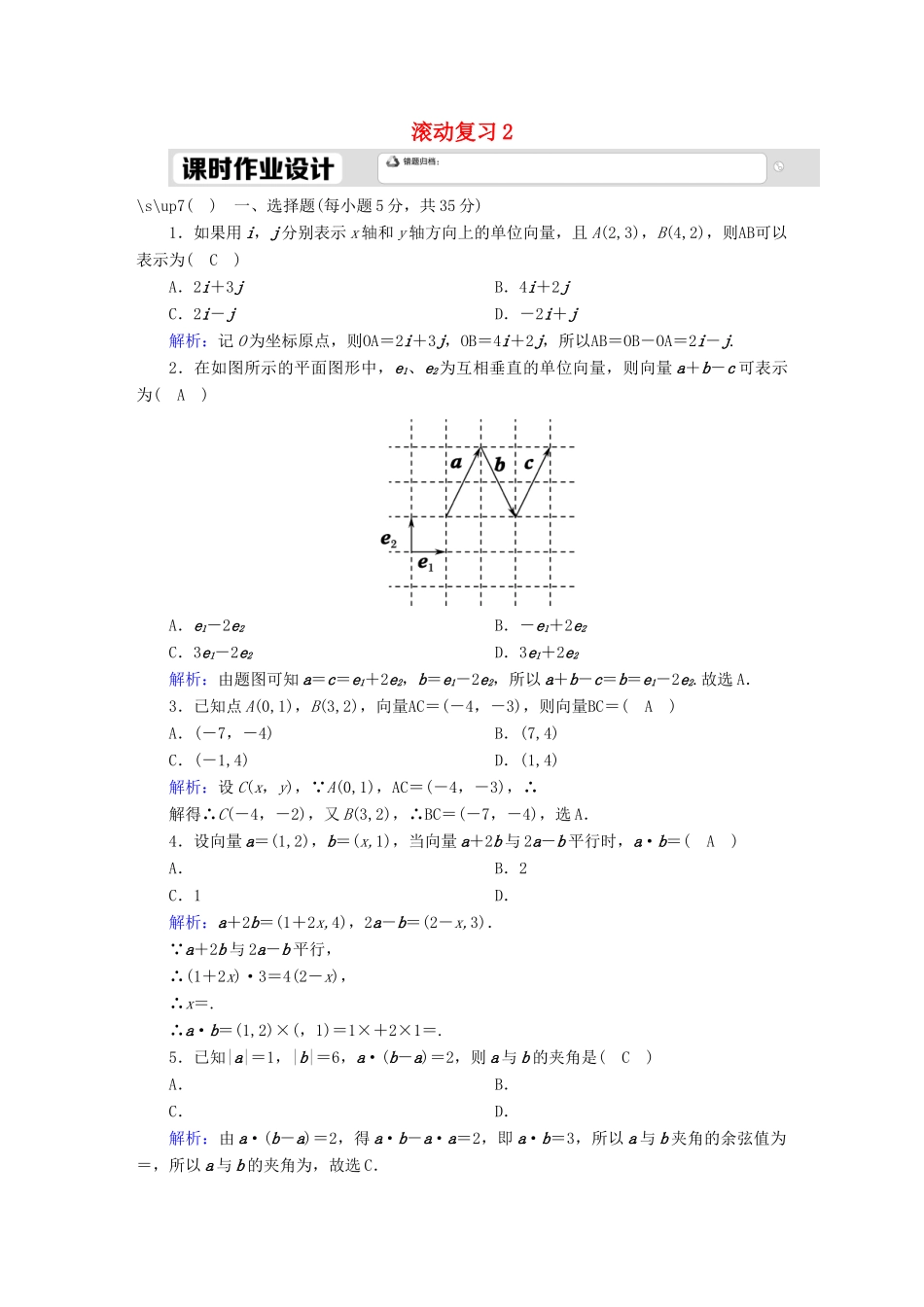
滚动复习2\s\up7()一、选择题(每小题5分,共35分)1.如果用i,j分别表示x轴和y轴方向上的单位向量,且A(2,3),B(4,2),则AB可以表示为(C)A.2i+3jB.4i+2jC.2i-jD.-2i+j解析:记O为坐标原点,则OA=2i+3j,OB=4i+2j,所以AB=OB-OA=2i-j.2.在如图所示的平面图形中,e1、e2为互相垂直的单位向量,则向量a+b-c可表示为(A)A.e1-2e2B.-e1+2e2C.3e1-2e2D.3e1+2e2解析:由题图可知a=c=e1+2e2,b=e1-2e2,所以a+b-c=b=e1-2e2.故选A.3.已知点A(0,1),B(3,2),向量AC=(-4,-3),则向量BC=(A)A.(-7,-4)B.(7,4)C.(-1,4)D.(1,4)解析:设C(x,y),∵A(0,1),AC=(-4,-3),∴解得∴C(-4,-2),又B(3,2),∴BC=(-7,-4),选A.4.设向量a=(1,2),b=(x,1),当向量a+2b与2a-b平行时,a·b=(A)A.B.2C.1D.解析:a+2b=(1+2x,4),2a-b=(2-x,3).∵a+2b与2a-b平行,∴(1+2x)·3=4(2-x),∴x=.∴a·b=(1,2)×(,1)=1×+2×1=.5.已知|a|=1,|b|=6,a·(b-a)=2,则a与b的夹角是(C)A.B.C.D.解析:由a·(b-a)=2,得a·b-a·a=2,即a·b=3,所以a与b夹角的余弦值为=,所以a与b的夹角为,故选C.6.如图,在圆O中,若弦AB=3,弦AC=5,则AO·BC的值等于(D)A.-8B.-1C.1D.8解析:取BC的中点D,连接OD,AD,则OD·BC=0且AO+OD=AD,即AO=AD-OD.∵AD=(AB+AC),∴AO·BC=AD·BC-OD·BC=AD·BC=(AB+AC)·(AC-AB)=(AC2-AB2)=×(52-32)=8.故选D.7.(多选)在平面直角坐标系中,已知三点A(a,2),B(3,b),C(2,3),O为坐标原点.若向量OB⊥AC,则a2+b2的取值可能是(BCD)A.B.C.12D.18解析:由题意得OB=(3,b),AC=(2-a,1),∵向量OB⊥AC,∴OB·AC=3(2-a)+b=0,∴b=3a-6,a2+b2=10a2-36a+36=10(a-)2+≥,当且仅当a=时,取等号.故选BCD.二、填空题(每小题5分,共20分)8.已知A(1,1),B(3,-1),C(a,b),若A,B,C三点共线,则a,b的关系式为__a+b=2__.解析:由已知AB=(2,-2),AC=(a-1,b-1),∵A,B,C三点共线,∴AB∥AC,∴2(b-1)+2(a-1)=0,即a+b=2.9.设a,b是两个不共线的非零向量,若向量ka+2b与8a+kb的方向相反,则k=__-4__;若方向相同,则k=__4__.解析:∵向量ka+2b与8a+kb的方向相反,∴ka+2b=λ·(8a+kb)⇒k=8λ,2=λk⇒k=-4(舍正),同理,方向相同,k=4.10.设向量a,b,c满足a+b+c=0,a⊥b,|a|=1,|b|=2,则|c|=.解析:由a+b+c=0,a⊥b,|a|=1,|b|=2,得c=-a-b,所以c2=(-a-b)2=a2+2a·b+b2=12+0+22=5,|c|=.11.如图,半径为1的扇形AOB的圆心角为120°,点C在上,且∠COB=30°.若OC=λOA+μOB,则λ+μ=.解析:由已知,可得OA⊥OC,以O为坐标原点,OC,OA所在直线分别为x轴、y轴建立平面直角坐标系,则有C(1,0),A(0,1),B(cos30°,-sin30°),即B(,-).于是OC=(1,0),OA=(0,1),OB=(,-),由OC=λOA+μOB,得(1,0)=λ(0,1)+μ(,-)=(μ,λ-μ),∴解得∴λ+μ=.三、解答题(共45分)12.(15分)在△ABC中,AB·AC=0,|AB|=12,|BC|=15,l为线段BC的垂直平分线,l与BC交于点D,E为l上异于D的任意一点.(1)求AD·CB的值;(2)判断AE·CB的值是否为一个常数,并说明理由.解:(1)∵AB·AC=0,∴AB⊥AC,又|AB|=12,|BC|=15,∴|AC|=9.由已知可得AD=(AB+AC),CB=AB-AC,∴AD·CB=(AB+AC)·(AB-AC)=(AB2-AC2)=×(144-81)=.(2)AE·CB的值为一个常数.理由如下:∵l为线段BC的垂直平分线,l与BC交于点D,E为l上异于D的任意一点,∴DE·CB=0,故AE·CB=(AD+DE)·CB=AD·CB+DE·CB=AD·CB=.13.(15分)已知正方形ABCD的边长为2,DE=2EC,DF=(DC+DB),求BE·DF的值.解:如图,以点B为原点,BC所在的直线为x轴,AB所在的直线为y轴建立平面直角坐标系.则B(0,0),E(2,),D(2,2).由DF=(DC+DB)知,点F为BC的中点,故DF=(-1,-2).∵BE=(2,),∴BE·DF=-2-=-.14.(15分)如图,A(0,5),O(0,0),B(4,3),OC=OA,OD=OB,AD与BC相交于点M,求点M的坐标.解:∵OC=OA=(0,5)=(0,),∴C(0,).∵OD=OB=(4,3)=(2,),∴D(2,).设M(x,y),则AM=(x,y-5),∵AM∥AD,AD=(2,-),∴-x-2(y-5)=0,即7x+4y=20.①又CM=(x,y-),CB=(4,).∵CM∥CB,∴x-4(y-)=0,即7x-16y=-20.②联立①②解得x=,y=2,故点M的坐标为(,2).