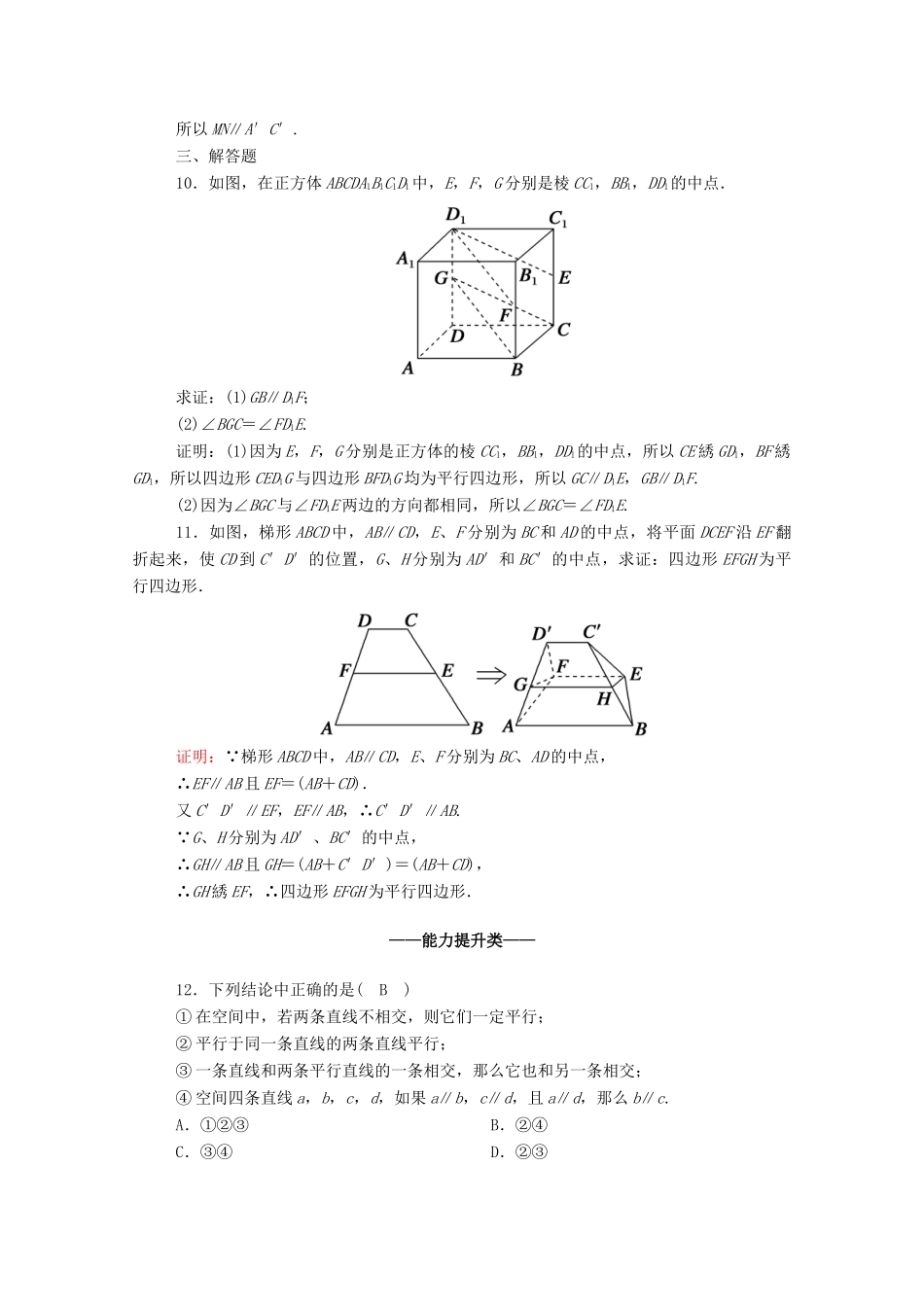
课时作业28直线与直线平行时间:45分钟——基础巩固类——一、选择题1.两等角的一组对应边平行,则(D)A.另一组对应边平行B.另一组对应边不平行C.另一组对应边不可能垂直D.以上都不对解析:另一组对应边可能平行,也可能不平行,也可能垂直.注意和等角定理(若两个角的对应边平行,则这两个角相等或互补)的区别.2.如图,在三棱柱ABCA1B1C1中,E,F,G分别为棱A1C1,B1C1,B1B的中点,则∠EFG与∠ABC1(B)A.相等B.互补C.相等或互补D.不确定解析:由于E,F,G分别为A1C1,B1C1,BB1的中点,所以EF∥A1B1∥AB,FG∥BC1,所以∠EFG与∠ABC1的两组对边分别平行,一组对应边方向相同,一组对应边方向相反,故∠EFG与∠ABC1互补.3.已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于(B)A.30°B.30°或150°C.150°D.大小无法确定解析:∠ABC的两边与∠PQR的两边分别平行,但方向不能确定是否相同,∴∠PQR=30°或150°.4.(多选)下列命题中,正确的结论有(BCD)A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等C.如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行解析:由等角定理得B、C正确,A错误,由基本事实4得D正确.5.如图所示,在长方体木块AC1中,E,F分别是B1O和C1O的中点,则长方体的各棱中与EF平行的有(B)A.3条B.4条C.5条D.6条解析:由于E、F分别是B1O、C1O的中点,故EF∥B1C1,因为和棱B1C1平行的棱还有3条:AD、BC、A1D1,所以共有4条.6.如图,在三棱锥PABC中,E,F,G,H,I,J分别为线段PA,PB,PC,AB,BC,CA的中点,则下列说法正确的是(C)A.PH∥BGB.IE∥CPC.FH∥GJD.GI∥JH解析:由题意结合三角形中位线的性质,可得FH∥PA,GJ∥PA,由基本事实4可得FH∥GJ.二、填空题7.已知空间两个角α,β,且α与β的两边对应平行,α=60°,则β为60°或120°.解析:根据“等角定理”可知,α与β相等或互补,故β为60°或120°.8.若AB∥A′B′,AC∥A′C′,则下列结论:①∠BAC=∠B′A′C′;②∠ABC+∠A′B′C′=180°;③∠ACB=∠A′C′B′或∠ACB+∠A′C′B′=180°.一定成立的是③.解析: AB∥A′B′,AC∥A′C′,∴∠ACB=∠A′C′B′或∠ACB+∠A′C′B′=180°.9.已知棱长为a的正方体ABCDA′B′C′D′中,M,N分别为CD,AD的中点,则MN与A′C′的位置关系是平行.解析:因为AN=DN,DM=MC,所以MN∥AC,因为AC∥A′C′,所以MN∥A′C′.三、解答题10.如图,在正方体ABCDA1B1C1D1中,E,F,G分别是棱CC1,BB1,DD1的中点.求证:(1)GB∥D1F;(2)∠BGC=∠FD1E.证明:(1)因为E,F,G分别是正方体的棱CC1,BB1,DD1的中点,所以CE綉GD1,BF綉GD1,所以四边形CED1G与四边形BFD1G均为平行四边形,所以GC∥D1E,GB∥D1F.(2)因为∠BGC与∠FD1E两边的方向都相同,所以∠BGC=∠FD1E.11.如图,梯形ABCD中,AB∥CD,E、F分别为BC和AD的中点,将平面DCEF沿EF翻折起来,使CD到C′D′的位置,G、H分别为AD′和BC′的中点,求证:四边形EFGH为平行四边形.证明: 梯形ABCD中,AB∥CD,E、F分别为BC、AD的中点,∴EF∥AB且EF=(AB+CD).又C′D′∥EF,EF∥AB,∴C′D′∥AB. G、H分别为AD′、BC′的中点,∴GH∥AB且GH=(AB+C′D′)=(AB+CD),∴GH綉EF,∴四边形EFGH为平行四边形.——能力提升类——12.下列结论中正确的是(B)①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线的一条相交,那么它也和另一条相交;④空间四条直线a,b,c,d,如果a∥b,c∥d,且a∥d,那么b∥c.A.①②③B.②④C.③④D.②③解析:①错,可以异面;②正确,基本事实4;③错误,和另一条可以异面;④正确,由平行直线的传递性可知.13.在空间四边形ABCD中,如图所示,=,=,则EH与FG的位置关系是平行.解析:如图,连接BD,在△ABD中,=,则EH∥BD,同理可得FG∥BD,∴EH∥FG.14.已知点E,E′分别是正方...