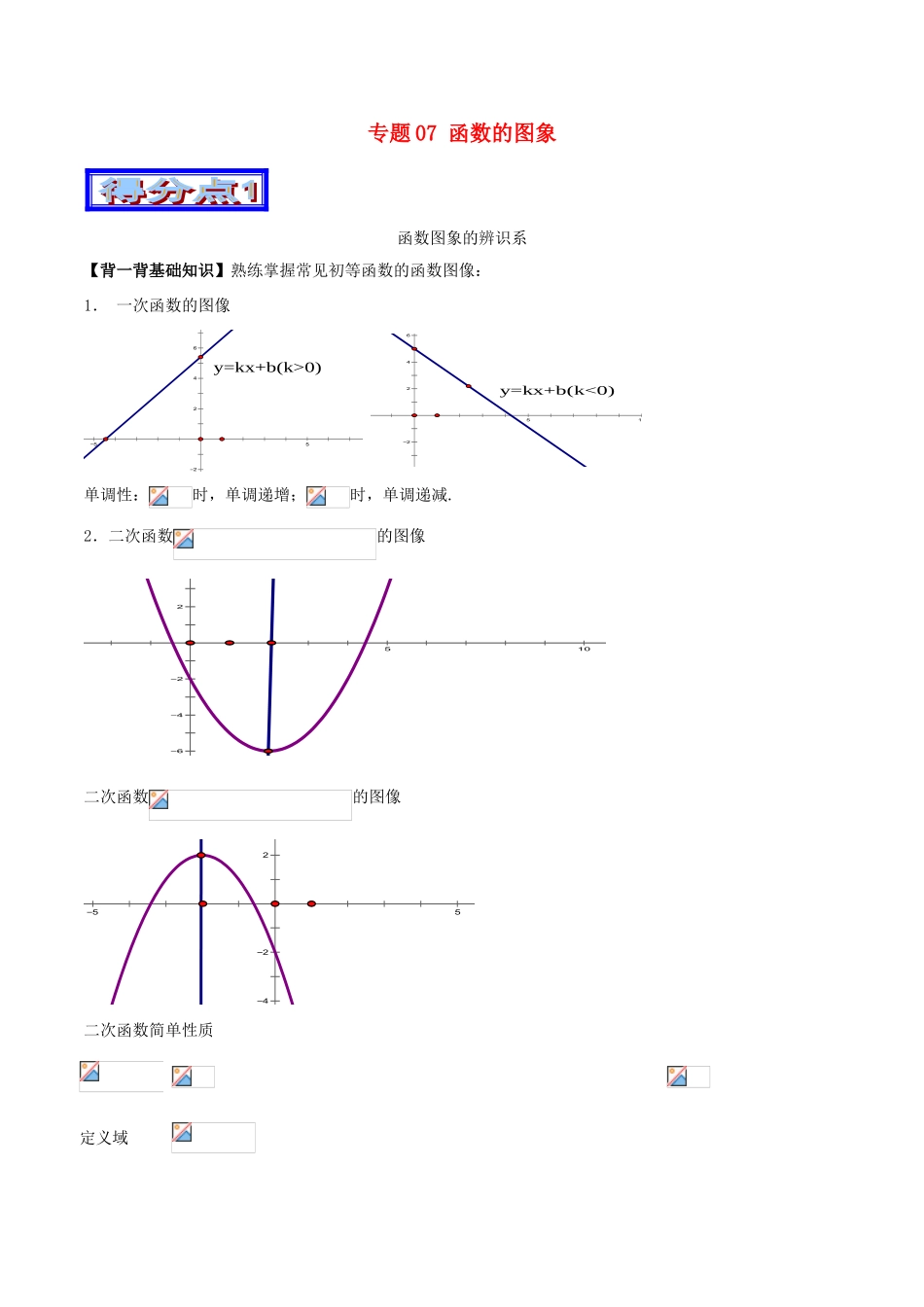
专题07函数的图象函数图象的辨识系【背一背基础知识】熟练掌握常见初等函数的函数图像:1.一次函数的图像642255y=kx+b(k>0)64224510y=kx+b(k<0)单调性:时,单调递增;时,单调递减.2.二次函数的图像2246510∙二次函数的图像22455二次函数简单性质定义域对称轴顶点坐标值域单调区间递减;递增递增;递减3.反比例函数422454225当时,图象分别位于第一、三象限,同一个象限内,随的增大而减小;当时,图象分别位于二、四象限,同一个象限内,随的增大而增大.4.指数函数图象1oyx逆时针旋转,底数越来越大逆时针旋转,底数越来越大性质定义域:值域:5.对数函数6.对角函数恒过点,即时,在上是增函数在上是减函数图象1oyx逆时针旋转,底数越来越小1oyx逆时针旋转,底数越来越小性质定义域:值域:恒过点,即当时,时,时时,时在上是增函数在上是减函数当时,(当且仅当即时取等号),由此可得函数(a>0,b>0,x∈R+)的性质:当时,函数有最小值,特别地,当时函数有最小值2.函数(a>0,b>0)在区间(0,)上是减函数,在区间(,+∞)上是增函数.因为函数(a>0,b>0)是奇函数,所以可得函数(a>0,b>0,x∈R-)的性质:当时,函数(a>0,b>0,x∈R-)有最大值-,特别地,当a=b=1时函数有最大值-2.函数(a>0,b>0)在区间(-∞,-)上是增函数,在区间(-,0)上是减函数.7.幂函数的图像与性质当时,幂函数有下列性质:(1)图象都通过点;(2)在第一象限内都是增函数;(3)在第一象限内,时,图象是向下凸的;时,图象是向上凸的;(4)在第一象限内,过点后,图象向右上方无限伸展.当时,幂函数有下列性质:(1)图象都通过点;(2)在第一象限内都是减函数,图象是向下凸的;(3)在第一象限内,图象向上与轴无限地接近;向右无限地与轴无限地接近;(4)在第一象限内,过点后,越大,图象下落的速度越快.【讲一讲基本技能】1.必备技能:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;(2)从函数的值域,判断图象的上下位置;(3)从函数的单调性,判断图象的变化趋势;(4)从函数的奇偶性,判断图象的对称性;(5)从函数的周期性,判断图象的循环往复.利用上述方法,排除、筛选错误与正确的选项.2.典型例题:例1函数的图象大致为()分析:本题考查的是对图像的识别,可抓住图像的某个特征,进行排除,进而可得真确答案.【答案】A例2已知反比例函数的图象经过点,当时,所对应的函数值的取值范围是【答案】分析:当时,所对应的函数值的取值范围,首先求出的值,由题意图象经过点,将点代入可求出,确定反比例函数的解析式为,根据反比例函数的性质得图象分布在第二、四象限,在每一象限,随的增大而增大,因为时,,所以当时,.正确理解反比例函数的增减性是解决本题的关键,结合函数的简图更易理解.22465(2,-1)2fx()=2x【练一练趁热打铁】1.已知的图象如图所示,则函数的图像是()【答案】A2.已知二次函数,则函数图像可能是()【答案】C函数图象的变换【背一背基础知识】1.平移变换(1)水平平移:函数的图像可以把函数的图像沿轴方向向左或向右平移个单位即可得到;(2)竖直平移:函数的图像可以把函数的图像沿轴方向向上或向下平移个单位即可得到.2.对称变换(1)函数的图像可以将函数的图像关于轴对称即可得到;(2)函数的图像可以将函数的图像关于轴对称即可得到;(3)函数的图像可以将函数的图像关于原点对称即可得到;(4)函数的图像可以将函数的图像关于直线对称得到.3.翻折变换:(1)函数的图像可以将函数的图像的轴下方部分沿轴翻折到轴上方,去掉原轴下方部分,并保留的轴上方部分即可得到;(2)函数的图像可以将函数的图像右边沿轴翻折到轴左边替代原轴左边部分并保留在轴右边部分即可得到.4.伸缩变换:(1)函数的图像可以将函数的图像中的每一点横坐标不变纵坐标伸长或压缩()为原来的倍得到;(2)函数的图像可以将函数的图像中的每一点纵坐标不变横坐标伸长或压缩()为原来的倍得到.5.具有对称性的抽象函数:①函数对于定义域中的任意,都有,则是关于直线对称的函数,②函数对于定义域中的任意,都有,则是关于点...