高中数学正、余二倍角公式的变式及其应用学法指导VIP免费

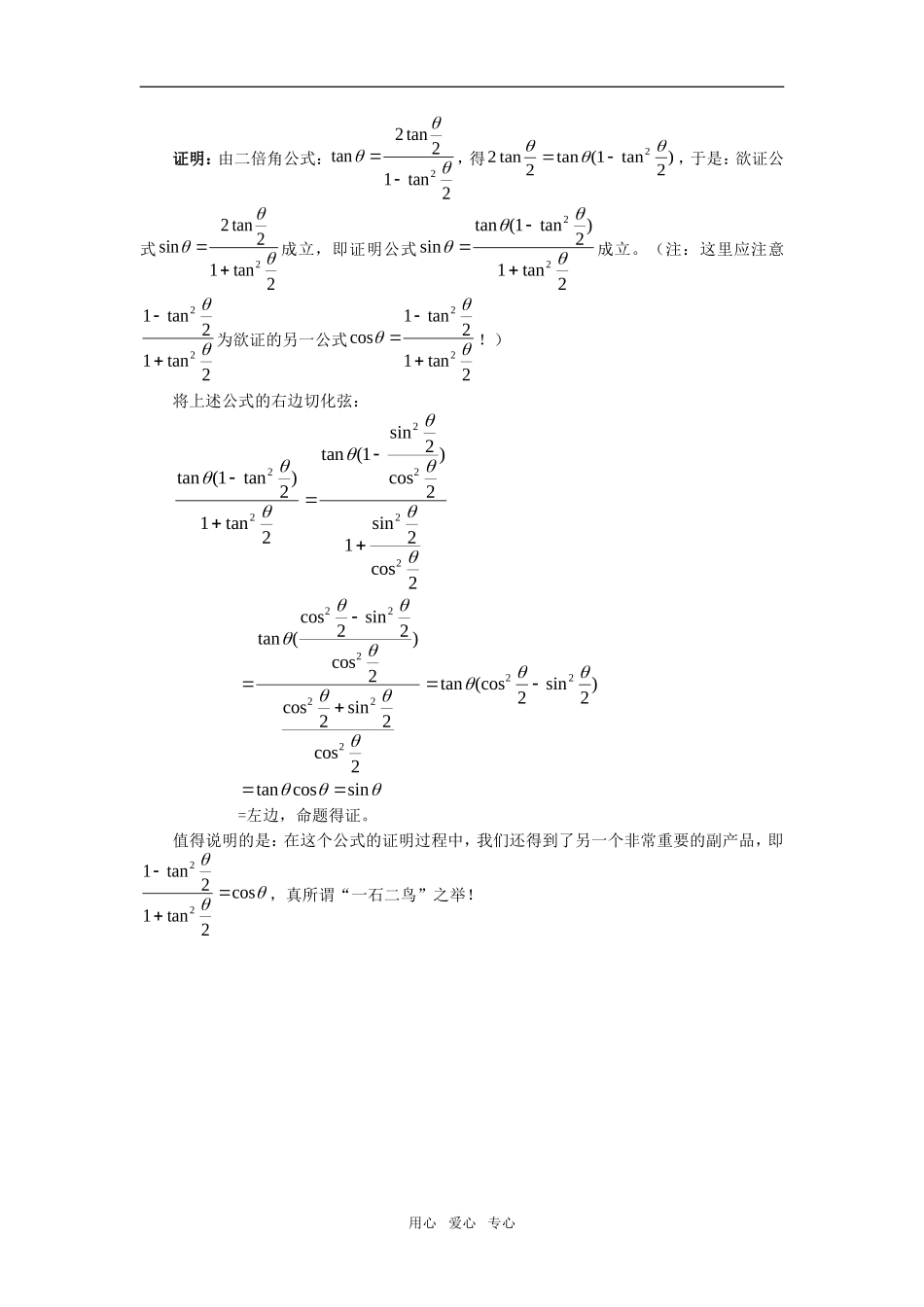
高中数学正、余二倍角公式的变式及其应用在三角函数的学习过程中，我们不仅要熟记一些常见的三角公式，而且要熟悉其变化形式，尤其是常用公式的变形公式，这对于提高我们思维的灵活性，开拓解题思路，会收到事半功倍的效果。下面通过对二倍角的正余弦公式的变形使用，加以说明。变形一sinsincoscossinsin2222例1求coscoscos204080的值。解：原式sinsinsinsinsinsin4022080240160280°sinsinsinsin1608202082018点评：本题中利用变形公式cossinsin22，使得问题得以巧解，简洁明快。另本题也可进行倍角变换，有如下解法：原式220204080220sincoscoscossinsincoscossinsincoscossinsincossinsincossinsinsinsinsin404080220240408022208080222028080222201608202082018变形二coscossincoscos22112122222sincos2122以及12212222coscoscossin，例2求证：844234coscoscos证明：左边812221224222222(cos)(cos)coscos242144423coscoscoscos右边例3（2002年全国高考题）已知sinsincoscos()2222102，，a，求sintan的值。解：由sinsincoscos2221得42120222sincossincos(cos)所以42202222sincossincoscos221022cos(sinsin)即221102cos(sin)(sin)因为a（，）02所以cossin01，所以210sin用心爱心专心即sincos1232，所以tan33所以sintan36点评：本题通过利用升幂公式：1222coscos，使得已知条件得以因式分解，进而使问题获解。变形三根据诱导公式，有sincos()cos()cossin2222422，()4，于是有二倍角公式的如下变形sinsin()cos()cos()sin()2441242412222cossin()cos()2244例4已知cos()sinsin()43524，求的值。解：因为cos()435所以sincos()sin()cos()212472544352，所以sinsin()2472535715例5已知sin()sin()()44162xxx，，，求sin4x的值。解：sin()sin()sin()cos()444416xxxx所以cossin()cos()224413xxx因为xx()()222，，所以，，所以sincos2122232xx所以sinsincos4222429xxx变形四对于正切二倍角公式：tantantan2221，通常也有如下变形：2tantan2(tan)tantantan112222，等等例6证明：万能公式：（1）sintantancostantan221221212222，（）。用心爱心专心证明：由二倍角公式：tantantan22122，得22122tantan(tan)，于是：欲证公式sintantan22122成立，即证明公式sintan(tan)tan121222成立。（注：这里应注意121222tantan为欲证的另一公式costantan121222！）将上述公式的右边切化弦：tan(tan)tantan(sincos)sincos1212122122222222tan(cossincos)cossincostan(cossin)tancossin2222222222222222=左边，命题得证。值得说明的是：在这个公式的证明过程中，我们还得到了另一个非常重要的副产品，即121222tantancos，真所谓“一石二鸟”之举！用心爱心专心