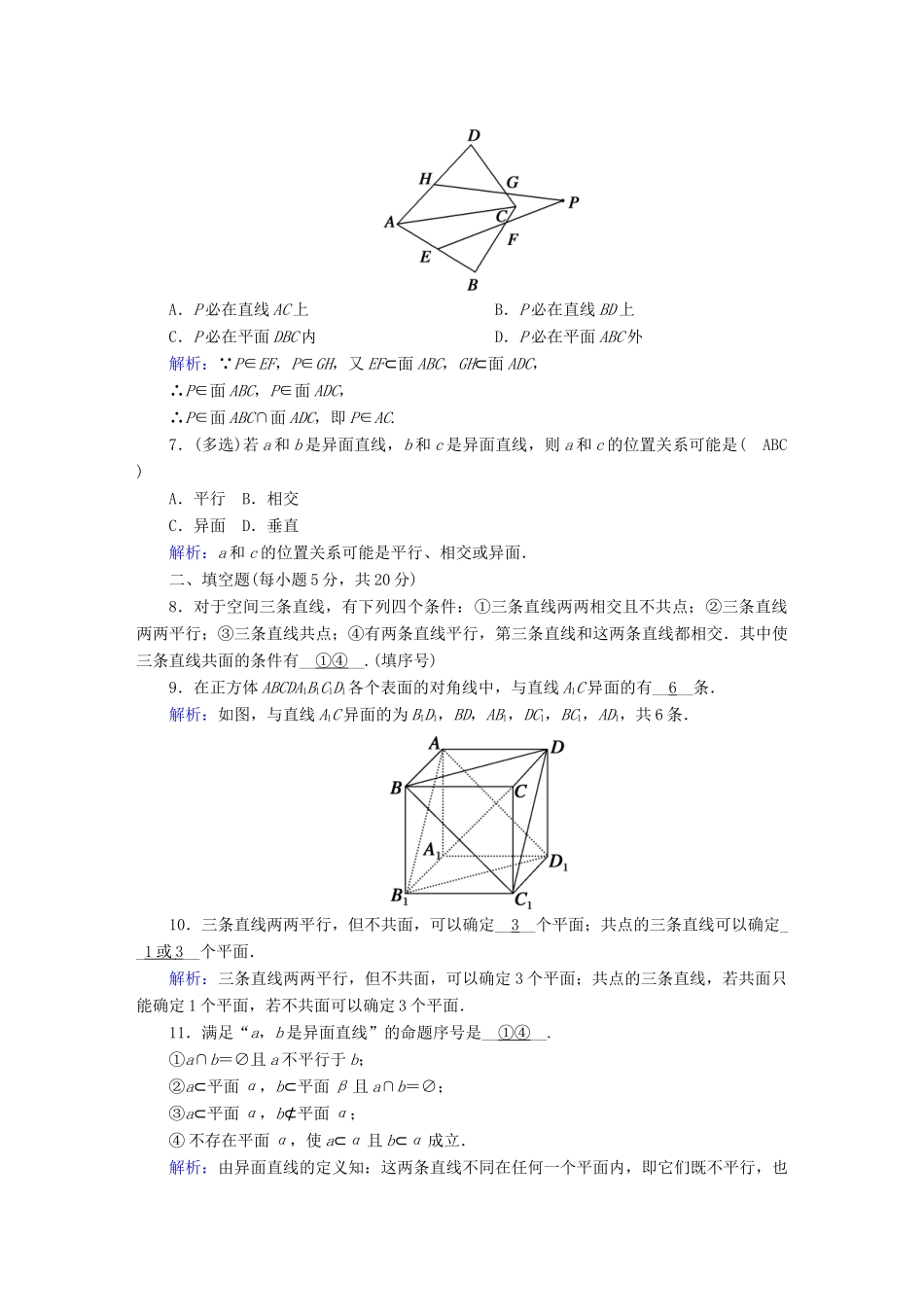
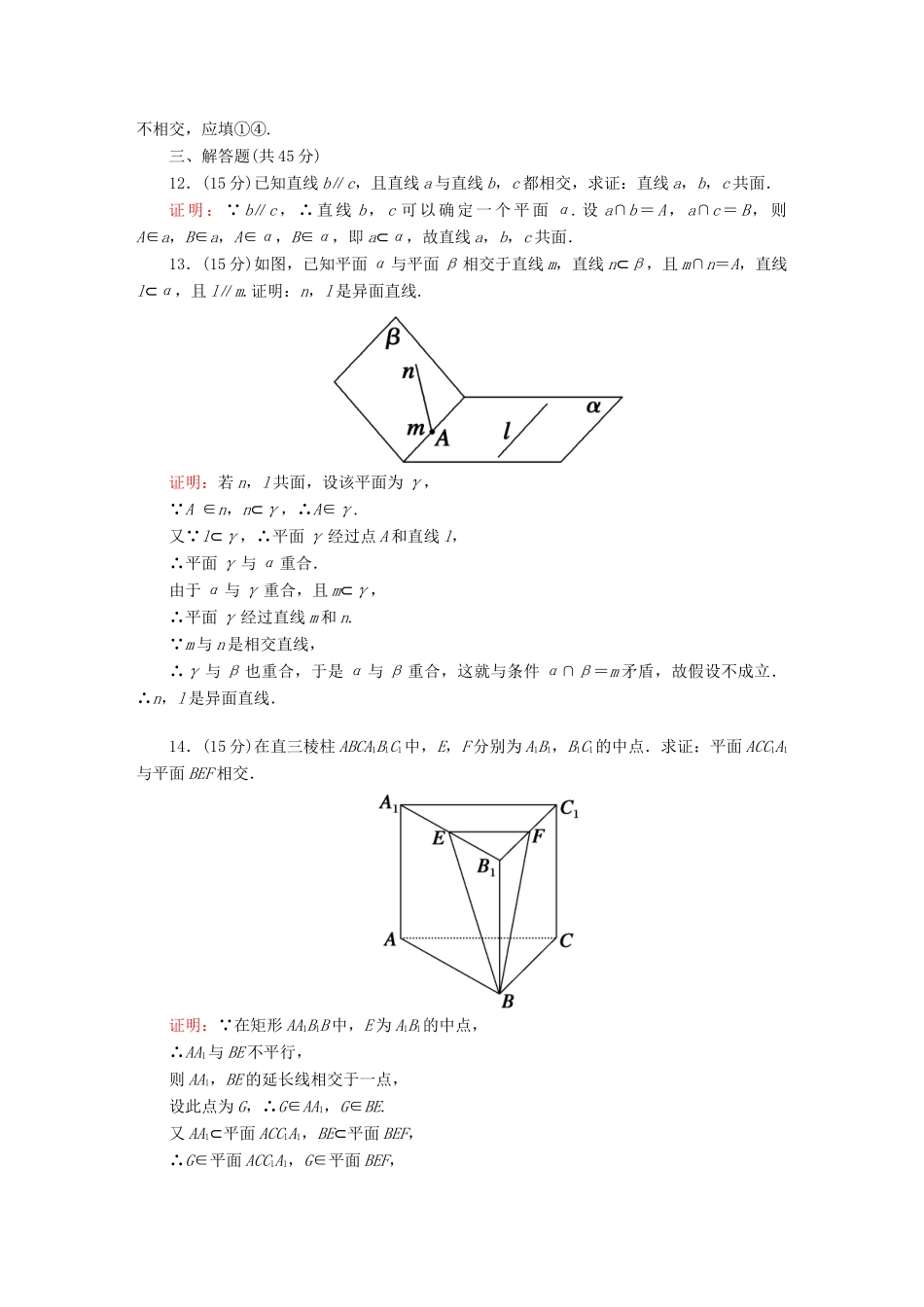
滚动复习7一、选择题(每小题5分,共35分)1.若点M在直线a上,a在平面α内,则M,a,α间的上述关系可记为(B)A.M∈a,a∈αB.M∈a,a⊂αC.M⊂a,a⊂αD.M⊂a,a∈α2.两个相交平面的画法,正确的是(D)解析:依据的是空间图形的画法要求及平面的基本性质.A不正确,因为图中没有标出两平面的交线;B不正确,在空间图形中,被某一平面遮住的部分应画成虚线或不画;C不正确,因为图形要表示两个相交平面,而不是要画两个平面四边形的摆放情况,两个相交平面必须相交于一条直线而不是一个点;D正确.3.已知下列说法:①三角形一定是平面图形;②若四边形的两条对角线相交于一点,则该四边形是平面图形;③三条平行线最多可确定三个平面.其中正确的有(C)A.1个B.2个C.3个D.0个解析:三个说法均正确.4.已知两条不同的直线a,b及两个不同的平面α,β,下列说法正确的是(C)A.若α∥β,a⊂α,b⊂β,则a∥bB.若α∥β,a⊂α,b⊂β,则a与b是异面直线C.若α∥β,a⊂α,b⊂β,则a与b平行或异面D.若α∩β=b,a⊂α,则a与β一定相交解析:分别在两个平行平面内的两条直线没有公共点,所以可能平行,也可能异面,C正确.5.下列说法正确的是(D)A.三点确定一个平面B.不重合的两个平面α和β可以有不在同一条直线上的三个公共点C.四边形一定是平面图形D.梯形一定是平面图形解析:因为不在同一直线上的三个点确定一个平面,所以A,B都错;对于C,在空间中四边形的四条边可能不在同一平面内,所以C错;对于D,由于平行的两条直线确定一个平面,而梯形是有一组对边平行的,所以梯形一定是平面图形,故D正确.6.在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,如图,如果EF、GH相交于点P,那么(A)A.P必在直线AC上B.P必在直线BD上C.P必在平面DBC内D.P必在平面ABC外解析:∵P∈EF,P∈GH,又EF⊂面ABC,GH⊂面ADC,∴P∈面ABC,P∈面ADC,∴P∈面ABC∩面ADC,即P∈AC.7.(多选)若a和b是异面直线,b和c是异面直线,则a和c的位置关系可能是(ABC)A.平行B.相交C.异面D.垂直解析:a和c的位置关系可能是平行、相交或异面.二、填空题(每小题5分,共20分)8.对于空间三条直线,有下列四个条件:①三条直线两两相交且不共点;②三条直线两两平行;③三条直线共点;④有两条直线平行,第三条直线和这两条直线都相交.其中使三条直线共面的条件有__①④__.(填序号)9.在正方体ABCDA1B1C1D1各个表面的对角线中,与直线A1C异面的有__6__条.解析:如图,与直线A1C异面的为B1D1,BD,AB1,DC1,BC1,AD1,共6条.10.三条直线两两平行,但不共面,可以确定__3__个平面;共点的三条直线可以确定__1或3__个平面.解析:三条直线两两平行,但不共面,可以确定3个平面;共点的三条直线,若共面只能确定1个平面,若不共面可以确定3个平面.11.满足“a,b是异面直线”的命题序号是__①④__.①a∩b=∅且a不平行于b;②a⊂平面α,b⊂平面β且a∩b=∅;③a⊂平面α,b⊄平面α;④不存在平面α,使a⊂α且b⊂α成立.解析:由异面直线的定义知:这两条直线不同在任何一个平面内,即它们既不平行,也不相交,应填①④.三、解答题(共45分)12.(15分)已知直线b∥c,且直线a与直线b,c都相交,求证:直线a,b,c共面.证明:∵b∥c,∴直线b,c可以确定一个平面α.设a∩b=A,a∩c=B,则A∈a,B∈a,A∈α,B∈α,即a⊂α,故直线a,b,c共面.13.(15分)如图,已知平面α与平面β相交于直线m,直线n⊂β,且m∩n=A,直线l⊂α,且l∥m.证明:n,l是异面直线.证明:若n,l共面,设该平面为γ,∵A∈n,n⊂γ,∴A∈γ.又∵l⊂γ,∴平面γ经过点A和直线l,∴平面γ与α重合.由于α与γ重合,且m⊂γ,∴平面γ经过直线m和n.∵m与n是相交直线,∴γ与β也重合,于是α与β重合,这就与条件α∩β=m矛盾,故假设不成立.∴n,l是异面直线.14.(15分)在直三棱柱ABCA1B1C1中,E,F分别为A1B1,B1C1的中点.求证:平面ACC1A1与平面BEF相交.证明:∵在矩形AA1B1B中,E为A1B1的中点,∴AA1与BE不平行,则AA1,BE的延长线相交于一点,设此点为G,∴G∈AA1,G∈BE.又AA1⊂平面ACC1A1,BE⊂平面BEF,∴G∈平面ACC1A1,G∈平面BEF,∴平面ACC1A1与平面BEF相交.