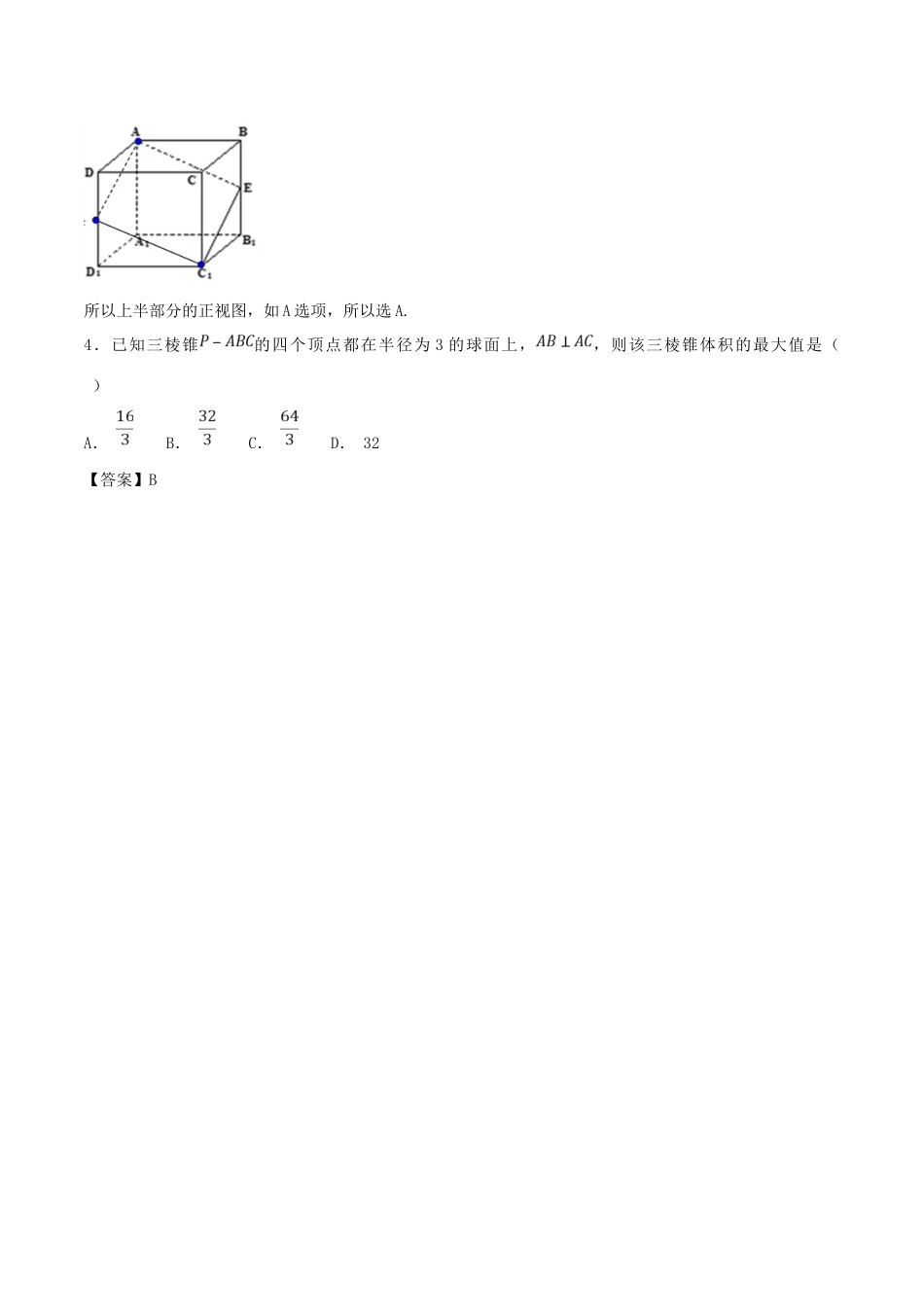
考点40空间几何体的三视图1.如图,在长方体中,,,而对角线上存在一点P,使得取得最小值,则此最小值为()A.2B.3C.D.【答案】D2.如图是某几何体的三视图,其中正视图和侧视图为正方形,俯视图是腰长为的等腰直角三角形,则该几何体的体积是()A.B.C.D.【答案】B3.如图,在正方体中,E为棱的中点,用过点的平面截去该正方体的上半部分,则剩余几何体的侧视图为A.B.C.D.【答案】C【解析】取中点F,连接.平面为截面。如下图:所以上半部分的正视图,如A选项,所以选A.4.已知三棱锥的四个顶点都在半径为3的球面上,,则该三棱锥体积的最大值是()A.B.C.D.32【答案】B在上递增,在上递减,,即该三棱锥体积的最大值是,故选B.5.如图,圆锥顶点为,底面圆心为,过轴的截面,为中点,,,则从点经圆锥侧面到点的最短距离为A.B.C.D.【答案】A6.已知三棱锥中,,,,,且二面角的大小为,则三棱锥外接球的表面积为()A.B.C.D.【答案】D,解得,外接球表面积故选D.7.某几何体的三视图如图所示,数量单位为,它的体积是()A.B.C.D.【答案】C8.在棱长为6的正方体ABCD-A1B1C1D1中,M是BC的中点,点P是正方形DCC1D1面内(包括边界)的动点,且满足∠APD=∠MPC,则三棱锥P-BCD的体积最大值是()A.36B.24C.D.【答案】D9.已知某几何体的三视图如图,则该几何体的表面积是()A.B.C.D.【答案】A【解析】几何体为圆锥挖掉个圆台.其表面积为:+42=.故选.10.正三棱锥S-ABC的外接球半径为2,底边长AB=3,则此棱锥的体积为A.B.或C.D.或【答案】B综上,棱锥的体积为或所以选B.11.如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,则该几何体外接球的表面积为()A.B.C.D.【答案】C12.九章算术是我国古代数学名著,在九章算术中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”,若某阳马”的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该“阳马”的表面积为A.B.C.D.【答案】C故选13.某几何体的三视图如图所示,则该几何体的外接球的表面积为()A.25πB.26πC.32πD.36π【答案】C14.某几何体的三视图如图所示,则该几何体的体积为A.1B.2C.3D.6【答案】B15.球面上有三点,,组成这个球的一个截面的内接三角形的三个顶点,其中,,,球心到这个截面的距离为球半径的一半,则球的表面积为()A.B.C.D.【答案】A【解析】,为直角三角形,其外接圆半径为,即截面的圆的半径为,又球心到截面的距离为,,,故选16.如图为某个几何体的三视图,则该几何体的外接球的表面积为()A.32πB.36πC.48πD.【答案】B17.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积为A.B.C.D.【答案】C18.如图,在四棱锥中,平面平面,,是等边三角形,已知,.(1)设是上的一点,证明:平面平面;(2)求四棱锥的体积.【答案】(1)证明见解析;(2).【解析】(1)证明:在中,由于,,,此即为梯形的高,所以四边形的面积为.故.19.如图,四边形为等腰梯形沿折起,使得平面平面为的中点,连接(如图2).图1图2(Ⅰ)求证:;(Ⅱ)求直线与平面所成的角的正弦值.【答案】(Ⅰ)证明见解析;(Ⅱ).20.已知所有棱长都相等的三棱锥的各个顶点同在一个半径为的球面上,则该三棱锥的表面积为___________.【答案】21.网格纸上小正方形的边长为1,粗虚、实线画出的是某个长方体挖去一个几何体得到的几何图形的三视图,则该被挖去的几何体的体积为__________.【答案】2【解析】根据三视图知长方体挖去部分是一个底面为等腰梯形(上底为2,下底为4,高为2)高为2的直四棱柱,所以.22.已知四面体的棱,,,则此四面体外接球的表面积__________.【答案】【解析】设BD的中点为O,23.已知棱长为1的正方体有一个内切球(如图),为面底的中心,与球相交于,则的长为_______.24.已知三棱柱的底面是正三角形,侧棱底面ABC,若有一半径为2的球与三棱柱的各条棱均相切,则的长度为______.【答案】【解析】25.已知棱长都相等正四棱锥的侧面...