广西北海二中高三数学理科测练（4）旧人教版VIP免费

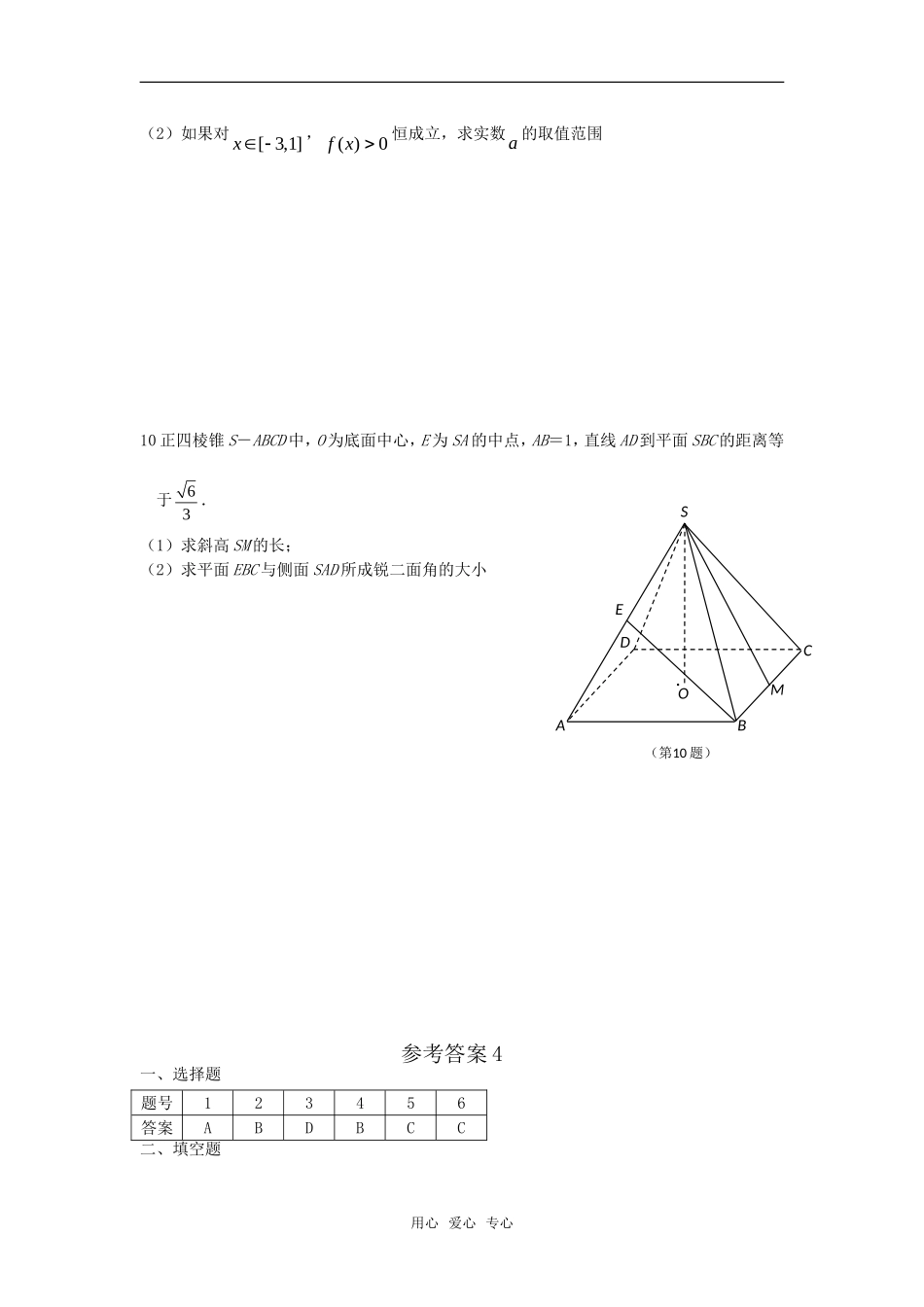
北海二中高三理科数学测练（4）（时间40分钟总分100分）班别：姓名：一、选择题（每题8分，共48分）1设命题甲：0＜x＜5；命题乙：|x-2|＜5，那么甲是乙的A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件2若4234012341234(12),xaaxaxaxaxaaaa则的值为A1B0C1D23设函数)(,3)()0(1)6sin()(xfxfxxf则的最大值为的导数的图象的一条对称轴的方程是A2xB6xC3xD9x4对于实数集R上可导函数fx，满足0xfx，则必有A.(1)201fffB.2011fffC.021fffD.021fff5函数122xxy的最小值为A0B43C1D．不存在6设函数()1xafxx，集合/{()0},{()0}MxfxPxfx，若MP，则实数a的取值范围是A(,1)B(0,1)C(1,)D[1,)题号123456答案二、填空题.（每题8分，共16分）7不等式2(1)(2)0(4)xxxx的解集为8设函数3,(10)()((5)),(10)xxfxffxx，则(5)f＝三、解答题（每题18分，共36分）9已知2()2(2)4fxxax，（1）如果对一切xR，()0fx恒成立，求实数a的取值范围；用心爱心专心（2）如果对[3,1]x，()0fx恒成立，求实数a的取值范围10正四棱锥S－ABCD中，O为底面中心，E为SA的中点，AB＝1，直线AD到平面SBC的距离等于63．（1）求斜高SM的长；（2）求平面EBC与侧面SAD所成锐二面角的大小参考答案4一、选择题题号123456答案ABDBCC二、填空题用心爱心专心SABCDOEM·（第10题）7、(,4)(0,2]{1}8、8三、解答题9解：（1）24(2)16004aa；（2）(2)3(3)0af或3(2)10a或(2)1(1)0af，解得a或14a或112a，∴a的取值范围为1(,4)210解法一：（1）连OM，作OH⊥SM于H．∵SM为斜高，∴M为BC的中点，∴BC⊥OM．∵BC⊥SM，∴BC⊥平面SMO．又OH⊥SM，∴OH⊥平面SBC．由题意，得166236OH．设SM＝x，则22611()622xx，解之32x，即32SM．（2）设面EBC∩SD＝F，取AD中点N，连SN，设SN∩EF＝Q．∵AD∥BC，∴AD∥面BEFC．而面SAD∩面BEFC＝EF，∴AD∥EF．又AD⊥SN，AD⊥NM，AD⊥面SMN．从而EF⊥面SMN，∴EF⊥QS，且EF⊥QM．∴∠SQM为所求二面角的平面角，记为α．由平几知识，得2222(2)2()QMSNMNMS．∴23342(1)44QM，∴114QM．∴221133()()1444cos11333244，即所求二面角为1arccos33．解法二：（1）建立空间坐标系（如图）∵底面边长为1，∴11(0)22A，，，11(0)22B，，，11(0)22C，，，1(00)2M，，．……………1分用心爱心专心SABCDOEMxyz（第10题）SABCDOEM·（第10题）QHFN设(00)Sh，，，平面SBC的一个法向(1)xy，，n，则1(0)2SMh�，，，(100)CB�，，．∴0CBx�n，102SMyh�n．∴y＝2h，n＝（0，2h，1）．…3分而AB�＝（0，1，0），由题意，得26||23||41ABhh�nn．解得22h．∴斜高223||2SMSOOM�．（2）n＝（0，2h，1）＝(021)，，，由对称性，面SAD的一个法向量为n1＝(021)，，．设平面EBC的一个法向量n2=（x，y，1），由112()444E，，，1321()(132)4444EB�，，，，，得22010(32).4CBxEBxy��，nn解得02.3xy，∴21(023)3，，n．设所求的锐二面角为α，则121212||1cos|cos|||||33，nnnnnn，∴1arccos33用心爱心专心