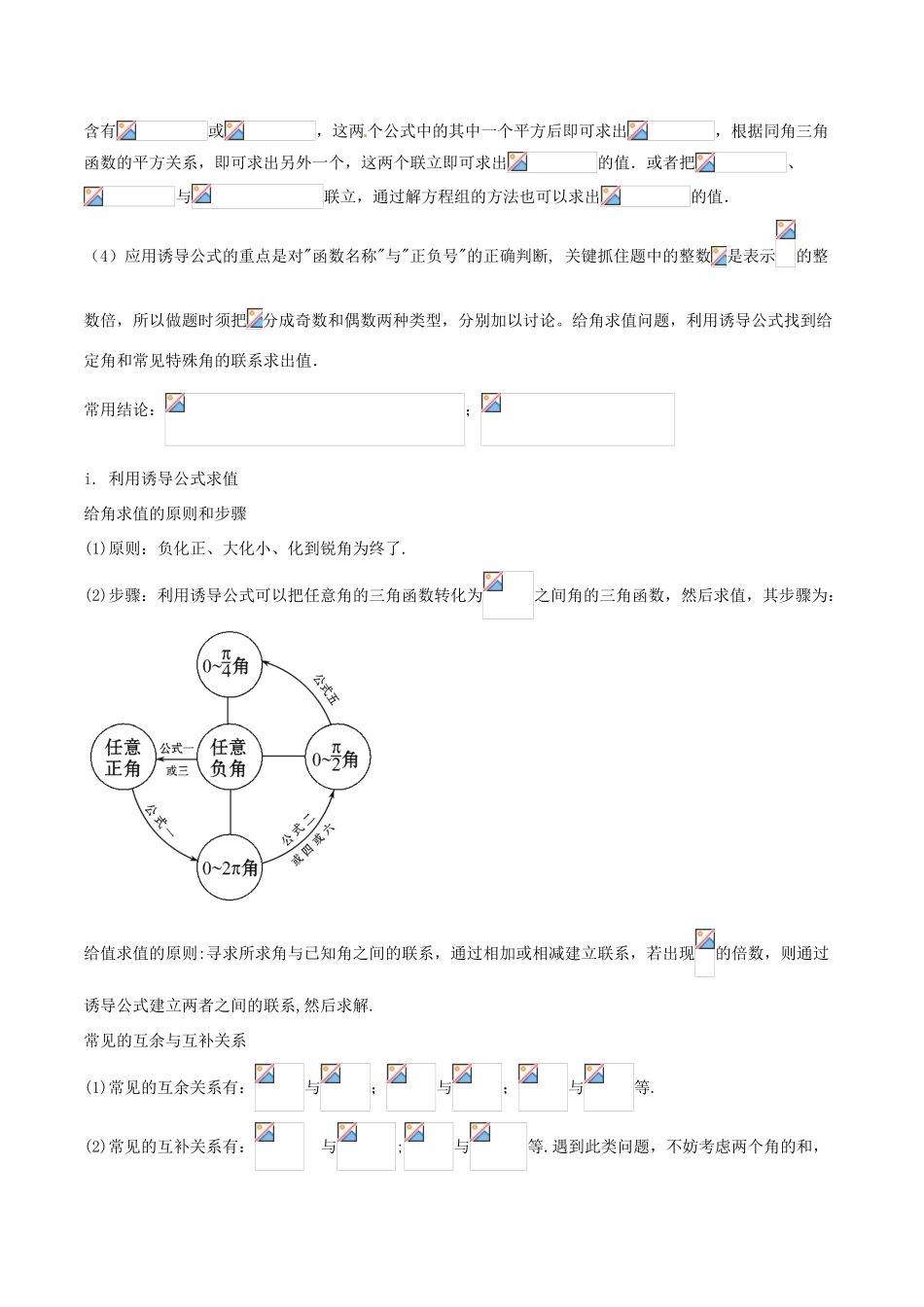
专题08三角函数同角三角函数的基本关系﹑诱导公式【背一背基础知识】1.掌握同角三角函数的基本关系式:,.2.诱导公式诱导公式一:,,,其中新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆诱导公式二:;,诱导公式三:;,诱导公式四:;,诱导公式五:;,诱导公式六:;,诱导公式七:;,-----------记忆方法:可用十个字概括为“奇变偶不变,符号看象限”,要把角化成形式为(为常整数);奇变偶不变是指:当为偶数时,三角函数名称不变,即前面若是正弦,后面也是正弦,名称不变,当为偶数时,三角函数名称变,即前面若是正弦,后面也是余弦,名称变;符号看象限是指:把看成锐角时,为第几象限角,由原三角函数在各象限符号决定正负号,具体一二象限正弦为正,一四象限余弦为正,一三象限正切为正,其它为负.【讲一讲基本技能】1.必备技能:(1)同角三角函数的基本关系式包括:(1)平方关系,(2)商数关系.解题时常用的变形措施有:大角化小,切割化弦等,应用“弦化切”的技巧,即分子、分母同除以一个不为零的,得到一个只含的教简单的三角函数式。需注意的是:①这是一组同角关系式,②利用平方关系式进行开方运算时,需注意运算结果的正负符号,③计算中应尽可能少用平方关系式.(2)正、余弦三兄妹“、”的应用与通过平方关系联系到一起,即,即(根据判断正负);因此在解题中若发现题设条件有三者之一,就可以利用上述关系求出或转化为另外两个.应用同角关系式的两点技巧:(1)"1"的代换:,(2)整体代换:为了计算或化简需要可将计算式作适当变形,使得所给条件可整体代入.(3)如何利用“切弦互化”技巧(1)弦化切:把正弦、余弦化成切得结构形式,这样减少了变量,统一为“切”得表达式,进行求值.常见的结构有:①的二次齐次式(如)的问题常采用“”代换法求解;②的齐次分式(如)的问题常采用分式的基本性质进行变形.(2)切化弦:利用公式,把式子中的切化成弦.一般单独出现正切、余切的时候,采用此技巧.温馨提示:(1)求同角三角函数有知一求三规律,可以利用公式求解,最好的方法是利用画直角三角形速解。(2)利用平方关系求三角函数值时,注意开方时要结合角的范围正确取舍“”号。的求值技巧:当已知,时,利用和、差角的三角函数公式展开后都含有或,这两个公式中的其中一个平方后即可求出,根据同角三角函数的平方关系,即可求出另外一个,这两个联立即可求出的值.或者把、与联立,通过解方程组的方法也可以求出的值.(4)应用诱导公式的重点是对"函数名称"与"正负号"的正确判断,关键抓住题中的整数是表示的整数倍,所以做题时须把分成奇数和偶数两种类型,分别加以讨论。给角求值问题,利用诱导公式找到给定角和常见特殊角的联系求出值.常用结论:;i.利用诱导公式求值给角求值的原则和步骤(1)原则:负化正、大化小、化到锐角为终了.(2)步骤:利用诱导公式可以把任意角的三角函数转化为之间角的三角函数,然后求值,其步骤为:给值求值的原则:寻求所求角与已知角之间的联系,通过相加或相减建立联系,若出现的倍数,则通过诱导公式建立两者之间的联系,然后求解.常见的互余与互补关系(1)常见的互余关系有:与;与;与等.(2)常见的互补关系有:与;与等.遇到此类问题,不妨考虑两个角的和,要善于利用角的变换的思想方法解决问题.ii.利用诱导公式化简、证明利用诱导公式化简三角函数的原则和要求(1)原则:遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行三角函数名称转化,以保证三角函数名称最少.(2)要求:①化简过程是恒等变形;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.iii.证明三角恒等式的主要思路(1)由繁到简法:由较繁的一边向简单一边化简.(2)左右归一法:使两端化异为同,把左右式都化为第三个式子.(3)转化化归法:先将要证明的结论恒等变形,再证明.提醒:由终边相同的角的关系可知,在计算含有的整数倍的三角函数式中可直接将的整数倍去掉后再进行运算,如.2.典型例题:例1已知...