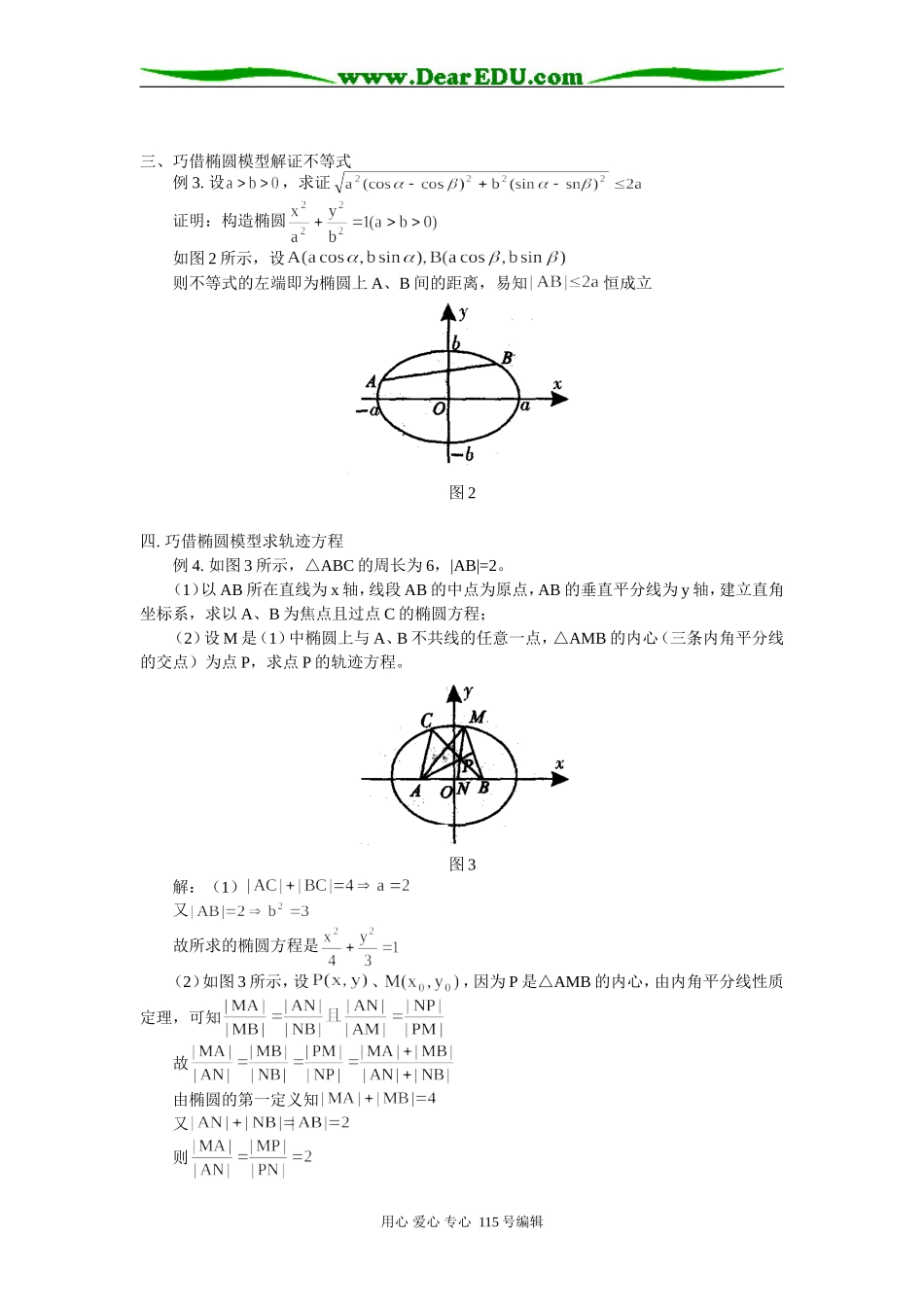
高中数学构造椭圆模型巧解题王卫华数学模型是采用数学语言表达数量关系,近似地表达出一种数学结构,它是解决数学问题的一种重要途径。其中构造椭圆模型解题就是比较典型的一类解题方法。一、巧借椭圆模型求最值例1.求函数的最值。解:设,则,所给函数可化为以u为参数的直线方程,它与椭圆在第一象限的部分(包括端点)有公共点,如图1所示。图1当直线与椭圆相切时,u取最大值,由△=0,得由题意知二、巧借椭圆模型求值域例2.求的值域。解:令则表示相对应的椭圆的上半部分,令问题转化为椭圆上半部分的一点,求的最值令,∴,即的值域为用心爱心专心115号编辑三、巧借椭圆模型解证不等式例3.设,求证证明:构造椭圆如图2所示,设则不等式的左端即为椭圆上A、B间的距离,易知恒成立图2四.巧借椭圆模型求轨迹方程例4.如图3所示,△ABC的周长为6,|AB|=2。(1)以AB所在直线为x轴,线段AB的中点为原点,AB的垂直平分线为y轴,建立直角坐标系,求以A、B为焦点且过点C的椭圆方程;(2)设M是(1)中椭圆上与A、B不共线的任意一点,△AMB的内心(三条内角平分线的交点)为点P,求点P的轨迹方程。图3解:(1)又故所求的椭圆方程是(2)如图3所示,设、,因为P是△AMB的内心,由内角平分线性质定理,可知故由椭圆的第一定义知又则用心爱心专心115号编辑由及椭圆性质知,由知点P分线段MN的比由定比分点公式知代入得点P的轨迹方程为用心爱心专心115号编辑