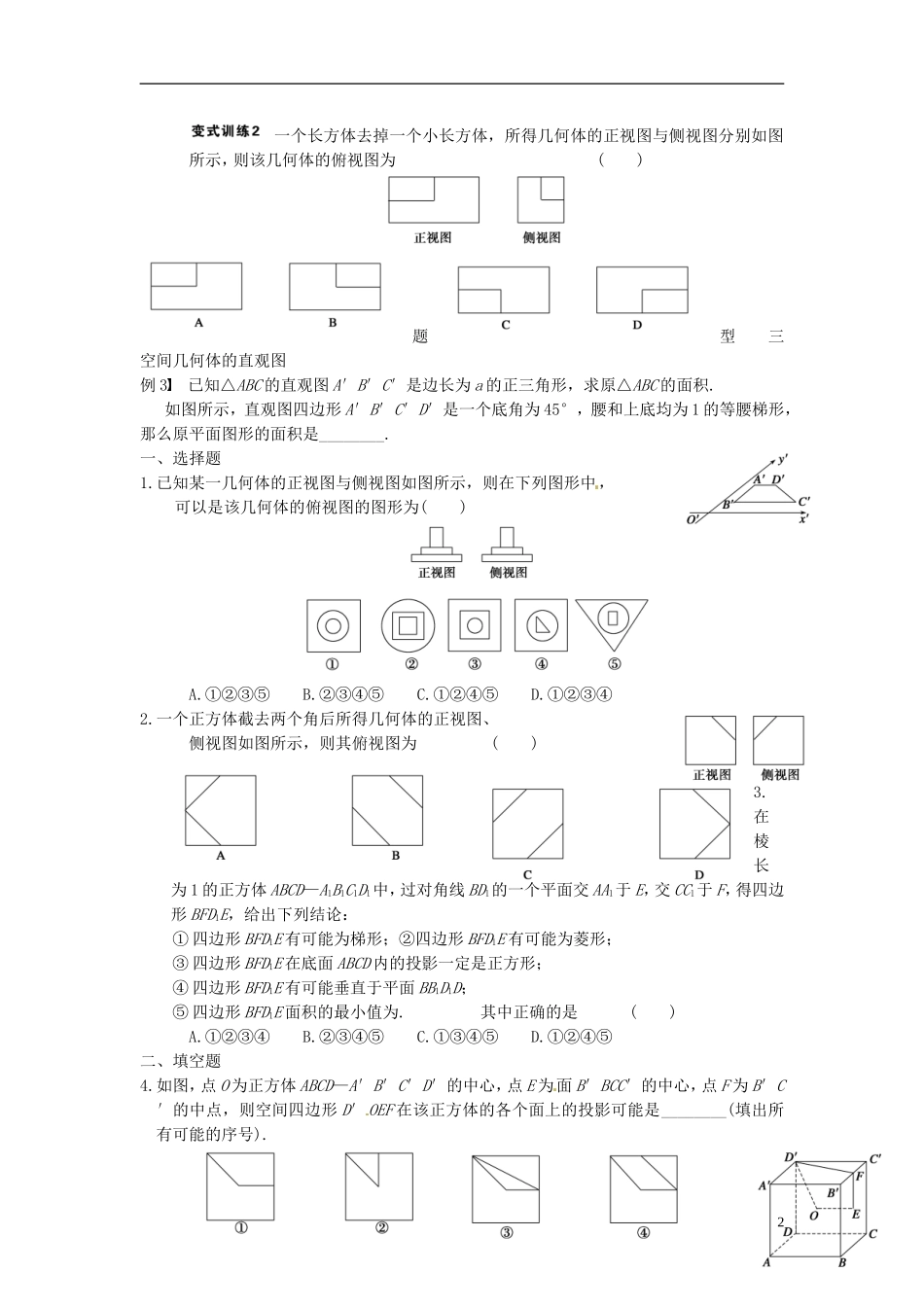
湖南省新田一中高中数学必修二强化训练:1-2空间几何体的结构及其三视1.多面体的结构特征(1)棱柱的上下底面________,侧棱都________且____________,上底面和下底面是________的多边形.(2)棱锥的底面是任意多边形,侧面是有一个____________的三角形.(3)棱台可由________________________的平面截棱锥得到,其上下底面的两个多边形________.2.旋转体的结构特征(1)圆柱可以由矩形绕其________________旋转得到.(2)圆锥可以由直角三角形绕其________________________________旋转得到.(3)圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上下底中点的连线旋转得到,也可由______________________的平面截圆锥得到.(4)球可以由半圆或圆绕其________旋转得到.3.空间几何体的三视图空间几何体的三视图是用__________得到,这种投影下与投影面平行的平面图形留下的影子与平面图形的形状和大小是____________的,三视图包括____________、__________、________.4.空间几何体的直观图画空间几何体的直观图常用________画法,基本步骤是:(1)在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′=__________.(2)已知图形中平行于x轴、y轴的线段,在直观图中分别平行于____________.(3)已知图形中平行于x轴的线段,在直观图中长度____________,平行于y轴的线段,长度变为______________.(4)在已知图形中过O点作z轴垂直于xOy平面,在直观图中对应的z′轴也垂直于x′O′y′平面,已知图形中平行于z轴的线段,在直观图中仍平行于z′轴且长度________.题型一空间几何体的结构特征例1设有以下四个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体;④棱台的相对侧棱延长后必交于一点.其中真命题的序号是________.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若过两个相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.其中,真命题的编号是________.题型二几何体的三视图例2已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为()1一个长方体去掉一个小长方体,所得几何体的正视图与侧视图分别如图所示,则该几何体的俯视图为()题型三空间几何体的直观图例3已知△ABC的直观图A′B′C′是边长为a的正三角形,求原△ABC的面积.如图所示,直观图四边形A′B′C′D′是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是________.一、选择题1.已知某一几何体的正视图与侧视图如图所示,则在下列图形中,可以是该几何体的俯视图的图形为()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④2.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示,则其俯视图为()3.在棱长为1的正方体ABCD—A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,得四边形BFD1E,给出下列结论:①四边形BFD1E有可能为梯形;②四边形BFD1E有可能为菱形;③四边形BFD1E在底面ABCD内的投影一定是正方形;④四边形BFD1E有可能垂直于平面BB1D1D;⑤四边形BFD1E面积的最小值为.其中正确的是()A.①②③④B.②③④⑤C.①③④⑤D.①②④⑤二、填空题4.如图,点O为正方体ABCD—A′B′C′D′的中心,点E为面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是________(填出所有可能的序号).25.对于四面体ABCD,下列命题正确的是________.(写出所有正确命题的编号)①相对棱AB与CD所在的直线异面;②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;③若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;④分别作三组相对棱中点的连线,所得的三条线段相交于一点;⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.6.用半径为r的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是________.三、解答题7.已知正三棱锥V—ABC的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图;(2)求出侧视图的面积.3