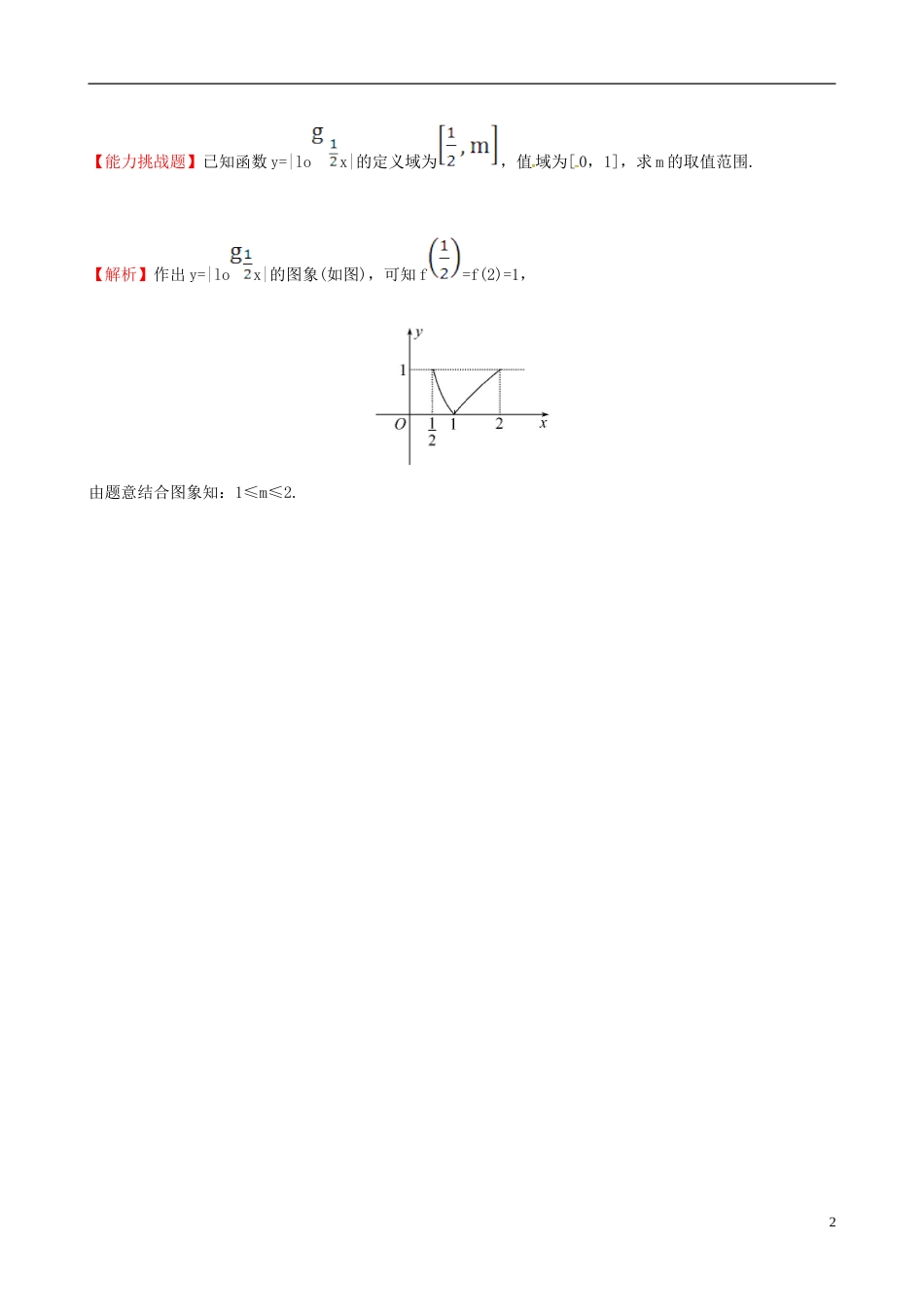
第二章基本初等函数(I)2.2.2对数函数及其性质第1课时对数函数的图象及性质课堂10分钟达标新人教版必修11.若f(x)=mlog2x为对数函数,则()A.m=1B.m=2C.m∈RD.m=-1【解析】选A.只有形如y=logax(a>0且a≠1)的函数,才是对数函数.2.若对数函数过点(4,2),则其解析式为()A.y=B.y=2xC.y=log4xD.y=log2x【解析】选D.设解析式为y=logax(a>0且a≠1),因为点(4,2)在对数函数图象上,故2=loga4,即a=2.3.函数f(x)=loga(2-x)的定义域为()A.(0,+∞)B.(2,+∞)C.(-∞,2)D.(-∞,0)【解析】选C.由题意2-x>0即x<2,故定义域为(-∞,2).4.若函数f(x)=loga+1x在(0,+∞)上单调递增,则a的取值范围为.【解析】因为f(x)在(0,+∞)上单调递增,所以a+1>1,即a>0.答案:a>05.函数f(x)=loga(x+1)+1(a>0且a≠1)的图象必经过定点.【解析】当x=0时,f(0)=loga1+1=1,所以图象必过定点(0,1).答案:(0,1)6.作出函数y=log2|x+1|的图象,由图象指出函数的单调区间,并说明它的图象可由y=log2x的图象经过怎样变换而得到.【解析】先作出函数y=log2x的图象,再作其关于y轴对称的图象,得到函数y=log2|x|的图象,再将图象向左平移1个单位长度就得到函数y=log2|x+1|的图象,如图所示.由图可得函数y=log2|x+1|的递减区间为(-∞,-1),递增区间为(-1,+∞).1【能力挑战题】已知函数y=|lox|的定义域为,值域为[0,1],求m的取值范围.【解析】作出y=|lox|的图象(如图),可知f=f(2)=1,由题意结合图象知:1≤m≤2.2