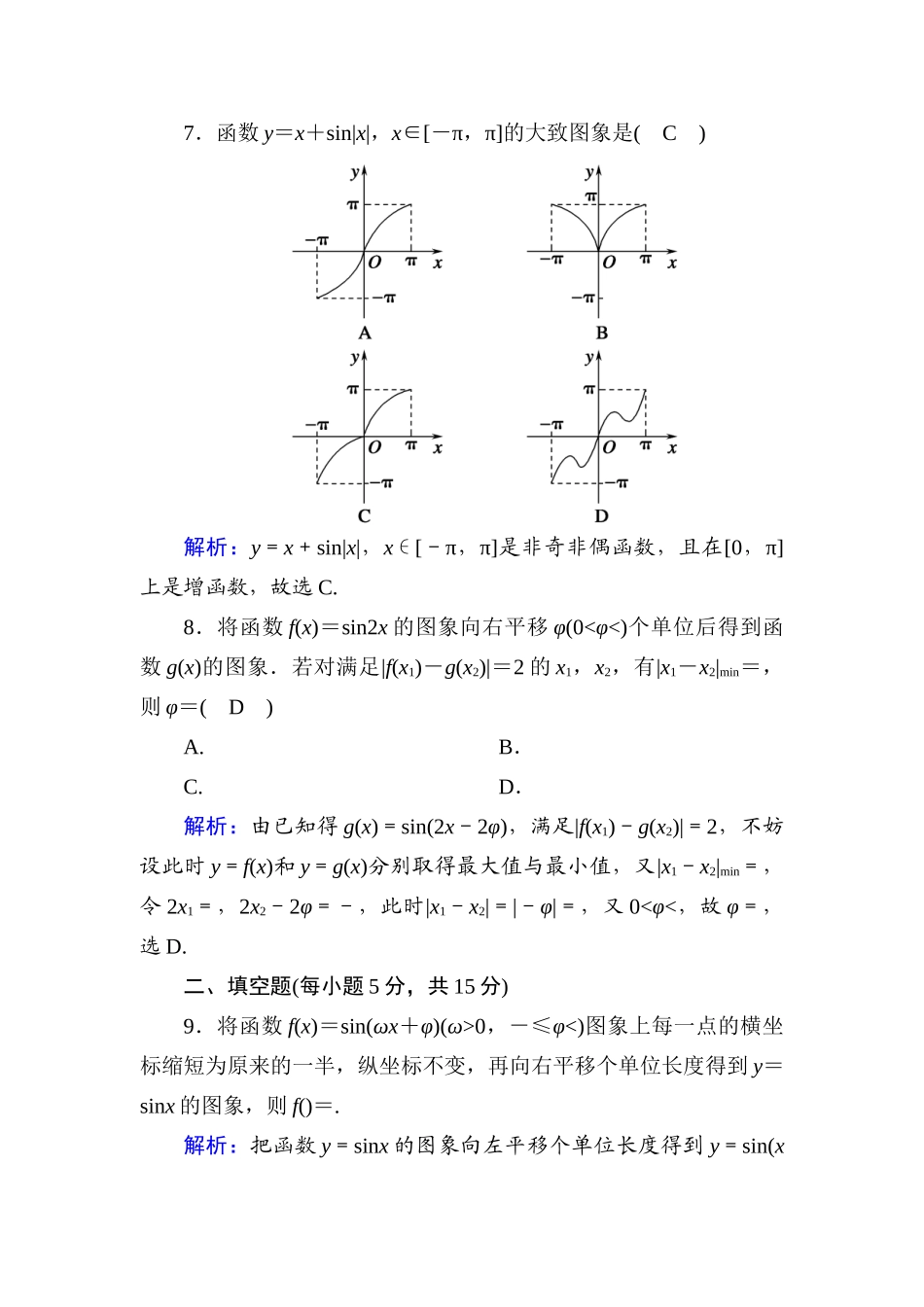
滚动复习12一、选择题(每小题5分,共40分)1.为了得到函数y=sin(x+1)的图象,只需把函数y=sinx的图象上所有的点(A)A.向左平行移动1个单位长度B.向右平行移动1个单位长度C.向左平行移动π个单位长度D.向右平行移动π个单位长度解析:由图象平移的规律“左加右减”,可知选A.2.要得到函数y=sin(4x-)的图象,只需将函数y=sin4x的图象(B)A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位解析:y=sin(4x-)=sin4(x-),故要将函数y=sin4x的图象向右平移个单位.故选B.3.已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<)在半个周期内的图象如图所示,则函数f(x)的解析式为(A)A.f(x)=2sin(x+)B.f(x)=2sin(2x-)C.f(x)=2sin(x-)D.f(x)=2sin(2x+)解析:本题主要考查通过三角函数图象求解函数的解析式.由图象知M=2.设函数f(x)的最小正周期为T,则T=-(-)=,可知T=2π,ω==1,将点(,2)代入f(x)的解析式得sin(+φ)=1,又|φ|<,可得φ=,故函数f(x)的解析式为f(x)=2sin(x+),故选A.4.把函数y=sin的图象向左平移个单位长度后,所得图象的一条对称轴的方程为(B)A.x=0B.x=C.x=-D.x=解析:把函数y=sin的图象向左平移个单位长度后,所得的图象的解析式为y=sin.由2x+=+kπ,k∈Z,得x=+kπ,k∈Z,故选B.5.函数y=Asin(ωx+φ)+k的部分图象如图所示,则该函数图象的振幅A与最小正周期T分别是(D)A.A=3,T=B.A=3,T=C.A=,T=D.A=,T=解析:由题图易知A=,T=-=,故T=π.6.将函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象经过点(,0),则ω的最小值是(D)A.B.1C.D.2解析:函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度得到函数g(x)=sin[ω(x-)](其中ω>0)的图象,将(,0)代入得0=sin,故ω的最小值是2.7.函数y=x+sin|x|,x∈[-π,π]的大致图象是(C)解析:y=x+sin|x|,x∈[-π,π]是非奇非偶函数,且在[0,π]上是增函数,故选C.8.将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=,则φ=(D)A.B.C.D.解析:由已知得g(x)=sin(2x-2φ),满足|f(x1)-g(x2)|=2,不妨设此时y=f(x)和y=g(x)分别取得最大值与最小值,又|x1-x2|min=,令2x1=,2x2-2φ=-,此时|x1-x2|=|-φ|=,又0<φ<,故φ=,选D.二、填空题(每小题5分,共15分)9.将函数f(x)=sin(ωx+φ)(ω>0,-≤φ<)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图象,则f()=.解析:把函数y=sinx的图象向左平移个单位长度得到y=sin(x+)的图象,再把函数y=sin(x+)图象上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到函数f(x)=sin(x+)的图象,所以f()=sin(×+)=sin=.10.已知函数f(x)=3sin(ωx-)(0<ω<3)的图象的一条对称轴是直线x=.若x∈[0,],则f(x)的值域是[-,3].解析:本题主要考查三角函数的图象和性质.依题意得ω-=kπ+(k∈Z),解得ω=3k+2(k∈Z),又 0<ω<3,∴ω=2,∴f(x)=3sin(2x-). x∈[0,],∴-≤2x-≤,∴-≤sin(2x-)≤1,∴-≤f(x)≤3.11.稳定房价是我国近年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.温州市某房地产中介对本市一楼群在今年的房价作了统计,发现每个季度的平均单价y(每平方米的价格,单位:元)与第x季度之间近似满足y=500sin(ωx+φ)+9500(ω>0),已知第一、二季度的平均单价如下表所示:x123y100009500?则此楼群在第三季度的平均单价大约是9_000元.解析:因为y=500sin(ωx+φ)+9500(ω>0),所以当x=1时,500sin(ω+φ)+9500=10000,当x=2时,500sin(2ω+φ)+9500=9500,解得ω=,φ=2kπ,k∈Z,所以y=500sinx+9500,当x=3时,y=9000.三、解答题(共45分)12.(15分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R)在一个周期内的图象如图所示,求直线y=与函数f(x)的图象的所有交点的坐标.解:由题图可得A=2,T=π-=4π,则...