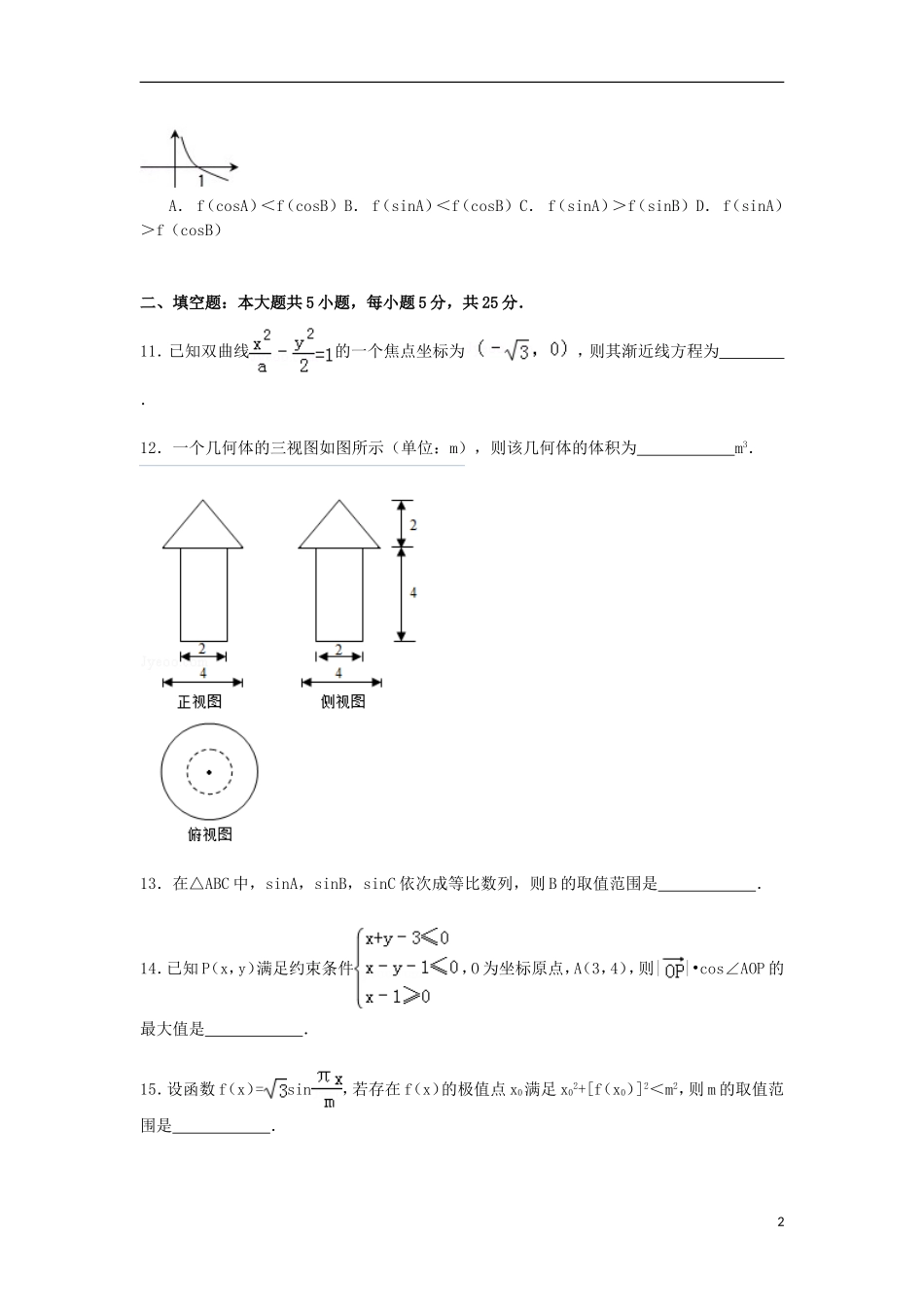
2014-2015学年山东省济南市济钢高中高三(上)1月月考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合P={log2x4,3},Q={x,y},若P∩Q={2},则P∪Q等于()A.{2,3}B.{1,2,3}C.{1,﹣1,2,3}D.{2,3,x,y}2.直线L的方向向量为M=(﹣1,2),直线L的倾角为α,则tan2α=()A.B.C.D.3.等差数列{an}前17项和S17=51,则a5﹣a7+a9﹣a11+a13=()A.3B.6C.17D.514.已知直线m,l和平面α、β,则α⊥β的充分条件是()A.m⊥l,m∥α,l∥βB.m⊥l,α∩β=m,l⊂αC.m∥l,m⊥α,l⊥βD.m∥l,l⊥β,m⊂α5.为了得到函数y=sin3x+cos3x的图象,可以将函数y=cos3x的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位6.设、都是非零向量,下列四个条件中,一定能使+=成立的是()A.=﹣B.∥C.=2D.⊥7.给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件8.某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是()A.72B.120C.144D.1689.设m∈R,过定点A的运直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P(x,y),则|PA|•|PB|的最大值是()A.4B.5C.6D.810.已知函数f(x)的导函数图象如图所示,若△ABC为锐角三角形,则一定成立的是()1A.f(cosA)<f(cosB)B.f(sinA)<f(cosB)C.f(sinA)>f(sinB)D.f(sinA)>f(cosB)二、填空题:本大题共5小题,每小题5分,共25分.11.已知双曲线的一个焦点坐标为,则其渐近线方程为.12.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.13.在△ABC中,sinA,sinB,sinC依次成等比数列,则B的取值范围是.14.已知P(x,y)满足约束条件,O为坐标原点,A(3,4),则||•cos∠AOP的最大值是.15.设函数f(x)=sin,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2,则m的取值范围是.2三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.16.已知函数,且函数f(x)的最小正周期为π.(Ⅰ)求函数f(x)的解析式;(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,若f(B)=1,=,且a+c=4,试求b2的值.17.已知圆C的圆心C在抛物线y2=8x的第一象限部分上,且经过该抛物线的顶点和焦点F(1)求圆C的方程(2)设圆C与抛物线的准线的公共点为A,M是圆C上一动点,求△MAF的面积的最大值.18.如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB>1,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2.(1)求证:D1E⊥A1D;(2)求AB的长度;(3)在线段AB上是否存在点E,使得二面角D1﹣EC﹣D的大小为.若存在,确定点E的位置;若不存在,请说明理由.19.观察下列三角形数表假设第n行的第二个数为an(n≥2,n∈N*).(Ⅰ)依次写出第六行的所有6个数字;(Ⅱ)归纳出an+1与an的关系式并求出an的通项公式;(Ⅲ)设anbn=1,求证:b2+b3+…+bn<2.20.函数f(x)=xlnx﹣ax2﹣x(a∈R).(I)若函数f(x)在x=1处取得极值,求a的值;(Ⅱ)若函数f(x)的图象在直线y=﹣x图象的下方,求a的取值范围;3(Ⅲ)求证:ln(2×3×…×2015)<2015.21.设椭圆C1:的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:y=x2﹣1与y轴的交点为B,且经过F1,F2点.(Ⅰ)求椭圆C1的方程;(Ⅱ)设M(0,),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求△MPQ面积的最大值.42014-2015学年山东省济南市济钢高中高三(上)1月月考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合P={log2x4,3},Q={x,y},若P∩Q={2},则P∪Q等于()A.{2,3}B.{1,2,3}C.{1,﹣1,2,3}D.{2,3,x,y}考点:...