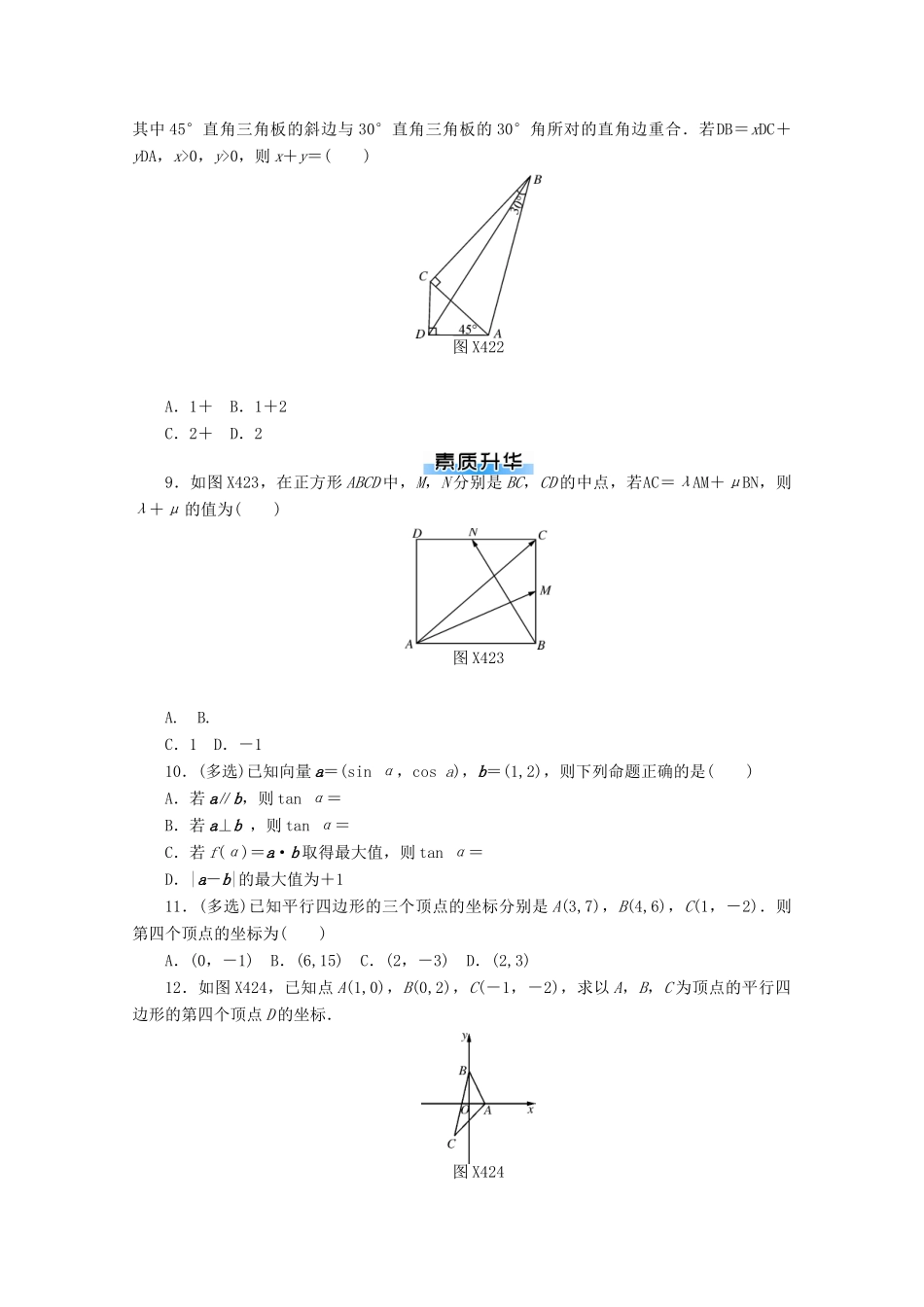
第2讲平面向量基本定理及坐标表示1.在平行四边形ABCD中,AC为一条对角线,若AB=(2,4),AC=(1,3),则BD=()A.(-2,-4)B.(-3,-5)C.(3,5)D.(2,4)2.已知直角坐标系内的两个向量a=(1,3),b=(m,2m-3)使平面内的任意一个向量c都可以唯一地表示成c=λa+μb,则m的取值范围是()A.(-∞,0)∪(0,+∞)B.(-∞,-3)∪(-3,+∞)C.(-∞,3)∪(3,+∞)D.[-3,3)3.在平行四边形ABCD中,E,F分别是BC,CD的中点,DE交AF于H,记AB,BC分别为a,b,则AH=()A.a-bB.a+bC.-a+bD.-a-b4.若向量α,β是一组基底,向量γ=xα+yβ(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标,现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为()A.(2,0)B.(0,-2)C.(-2,0)D.(0,2)5.将函数y=3sin的图象按向量a=平移后所得图象的解析式是()A.y=3sin-1B.y=3sin+1C.y=3sin2x+1D.y=3sin-16.(2017年重庆一模)已知△ABC的外接圆半径为2,D为该圆上的一点,且AB+AC=AD,则△ABC的面积的最大值为()A.3B.4C.3D.47.(2017年江苏)如图X421,在同一个平面内,向量OA,OB,OC的模分别为1,1,,OA与OC的夹角为α,且tanα=7,OB与OC的夹角为45°.若OC=mOA+nOB(m,n∈R),则m+n=________.图X4218.(2018年四川南充诊断)如图X422,将45°直角三角板和30°直角三角板拼在一起,其中45°直角三角板的斜边与30°直角三角板的30°角所对的直角边重合.若DB=xDC+yDA,x>0,y>0,则x+y=()图X422A.1+B.1+2C.2+D.29.如图X423,在正方形ABCD中,M,N分别是BC,CD的中点,若AC=λAM+μBN,则λ+μ的值为()图X423A.B.C.1D.-110.(多选)已知向量a=(sinα,cosa),b=(1,2),则下列命题正确的是()A.若a∥b,则tanα=B.若a⊥b,则tanα=C.若f(α)=a·b取得最大值,则tanα=D.|a-b|的最大值为+111.(多选)已知平行四边形的三个顶点的坐标分别是A(3,7),B(4,6),C(1,-2).则第四个顶点的坐标为()A.(0,-1)B.(6,15)C.(2,-3)D.(2,3)12.如图X424,已知点A(1,0),B(0,2),C(-1,-2),求以A,B,C为顶点的平行四边形的第四个顶点D的坐标.图X42413.若点M是△ABC所在平面内一点,且满足AM=AB+AC.(1)求△ABM与△ABC的面积之比;(2)若N为AB中点,AM与CN交于点O,设BO=xBM+yBN,求x,y的值.第2讲平面向量基本定理及坐标表示1.B解析:由题意,得BD=AD-AB=BC-AB=(AC-AB)-AB=AC-2AB=(1,3)-2(2,4)=(-3,-5).2.B解析:由题意可知,向量a与b为基底,∴不共线,≠,得m≠-3,故选B.3.B解析:方法一,如图D147,设AH=λAF,DH=μDE. DH=DA+AH=-b+λAF=-b+λ(b+a),又DH=μDE=μ(a-b),∴μ(a-b)=-b+λ(b+a).由于a,b不共线,因此由平面向量基本定理,得解得λ=,μ=.故AH=λAF=λ(b+a)=a+b.故选B.图D147图D148方法二,如图D148,作FM∥BC交ED于M,∴MF∥AD. E,F分别为BC,DC的中点,∴===,即AH=AF.∴AH=AF==AB+AD=a+b.故选B.4.D解析: a在基底p,q下的坐标为(-2,2),即a=-2p+2q=(2,4).令a=xm+yn=(-x+y,x+2y),∴即∴a在基底m,n下的坐标为(0,2).故选D.5.A解析:将函数y=3sin的图象按向量a=平移即向左平移个单位,再向下移动1个单位.6.B解析:由题设AB+AC=AD,可知四边形ABDC是平行四边形.由圆内接四边形的性质,可知∠BAC=90°,且当AB=AC时,四边形ABDC的面积最大,则△ABC的面积的最大值为Smax=AB×ACsin90°=×2=4.故选B.7.3解析:由tanα=7,得sinα=,cosα=.根据向量的分解,易得即解得∴m+n=3.8.B解析:如图D149建立平面直角坐标系,不妨设DA=DC=1,则AC=.AB=2,BC=,作BH⊥y轴于H,又∠HCB=45°,∴CH=HB=,∴B(,+1),即DB=(,+1),又DC=(0,1),DA=(1,0),DB=xDC+yDA,∴x+y=(+1)+=2+1.故选B.图D1499.A解析:方法一,记AB=a,BC=b,则AC=a+b,⇒∴AC=AM+BN,又AC=λAM+μBN,∴λ=,μ=,故λ+μ=,故选A.方法二(坐标法),如图D150建...