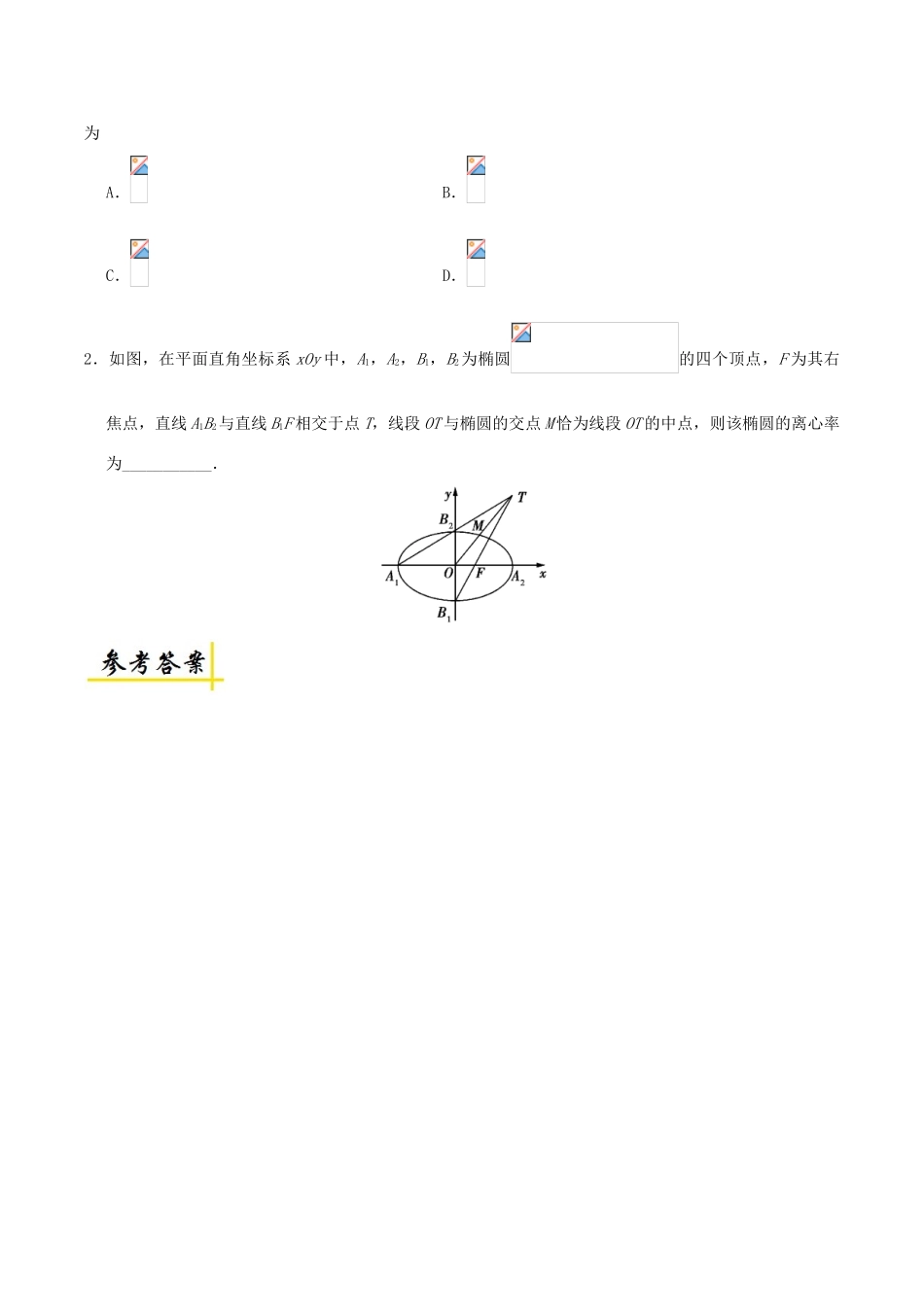
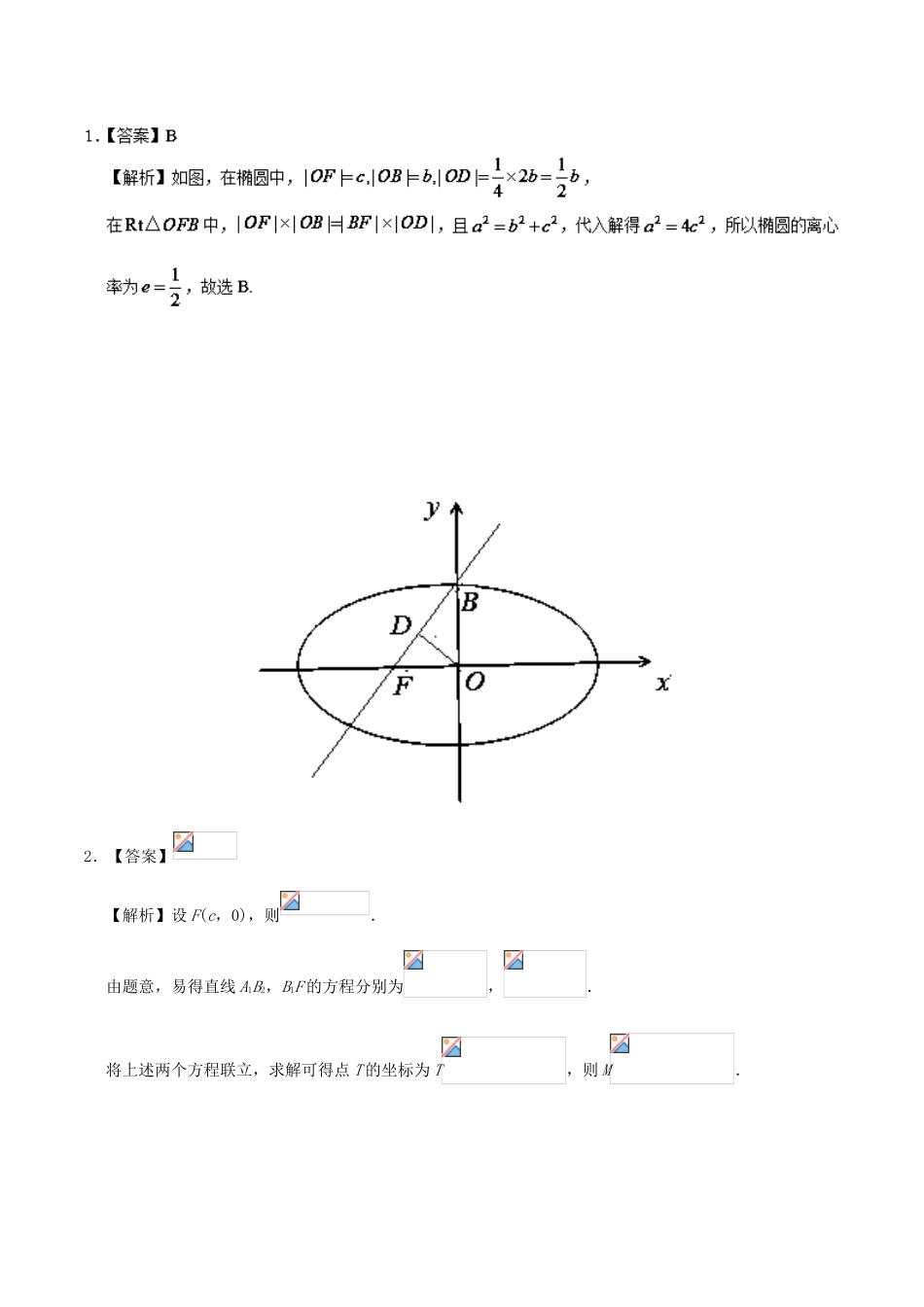
椭圆的简单几何性质(2)高考频度:★★★★☆难易程度:★★★☆☆典例在线正方形的四个顶点都在椭圆上,若椭圆的焦点在正方形的内部,则椭圆的离心率的取值范围是A.B.C.D.【参考答案】B【解题必备】本题主要考查利用椭圆的简单几何性质求椭圆的离心率,属于中档题.求解与椭圆性质有关的问题时要结合图形进行分析,即使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、长轴、短轴、离心率等椭圆的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.求离心率范围问题时应先将与有关的一些量表示出来,再利用其中的一些关系构造出关于的不等式,从而求出的范围.本题是利用椭圆的焦点在正方形的内部,构造出关于的不等式,最后解出的范围.学霸推荐1.直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为A.B.C.D.2.如图,在平面直角坐标系xOy中,A1,A2,B1,B2为椭圆的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为___________.2.【答案】【解析】设F(c,0),则.由题意,易得直线A1B2,B1F的方程分别为,.将上述两个方程联立,求解可得点T的坐标为T,则M.又点M在椭圆上,所以,整理得,两边同时除以,可得,解得或(舍去).