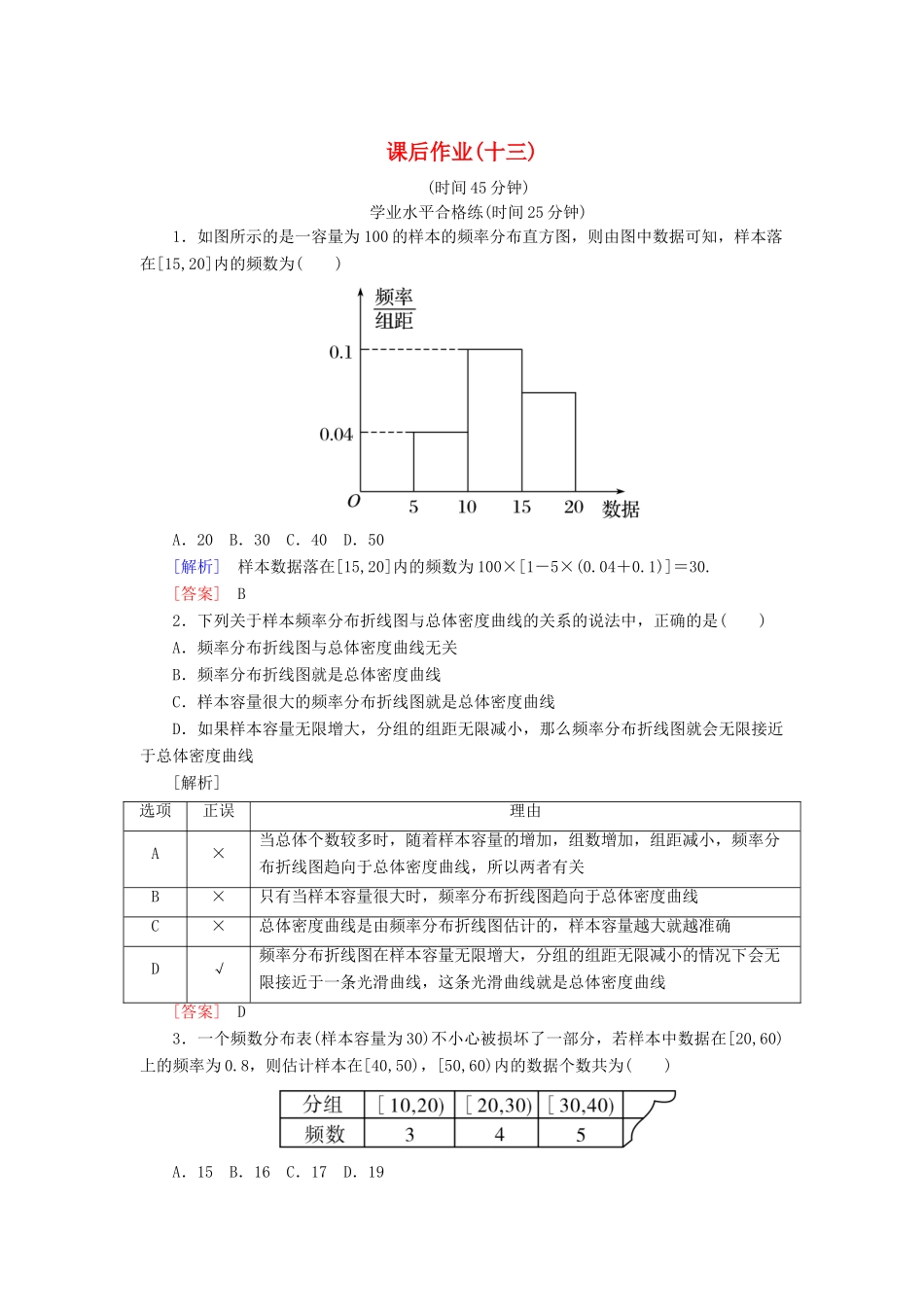
课后作业(十三)(时间45分钟)学业水平合格练(时间25分钟)1.如图所示的是一容量为100的样本的频率分布直方图,则由图中数据可知,样本落在[15,20]内的频数为()A.20B.30C.40D.50[解析]样本数据落在[15,20]内的频数为100×[1-5×(0.04+0.1)]=30.[答案]B2.下列关于样本频率分布折线图与总体密度曲线的关系的说法中,正确的是()A.频率分布折线图与总体密度曲线无关B.频率分布折线图就是总体密度曲线C.样本容量很大的频率分布折线图就是总体密度曲线D.如果样本容量无限增大,分组的组距无限减小,那么频率分布折线图就会无限接近于总体密度曲线[解析]选项正误理由A×当总体个数较多时,随着样本容量的增加,组数增加,组距减小,频率分布折线图趋向于总体密度曲线,所以两者有关B×只有当样本容量很大时,频率分布折线图趋向于总体密度曲线C×总体密度曲线是由频率分布折线图估计的,样本容量越大就越准确D√频率分布折线图在样本容量无限增大,分组的组距无限减小的情况下会无限接近于一条光滑曲线,这条光滑曲线就是总体密度曲线[答案]D3.一个频数分布表(样本容量为30)不小心被损坏了一部分,若样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数共为()A.15B.16C.17D.19[解析]由题意得,样本在[40,50),[50,60)内的数据个数共为30×0.8-4-5=15.[答案]A4.某厂对一批产品进行抽样检测,如图是抽检产品净重(单位:克)的频率分布直方图,样本数据分组为[76,78),[78,80),…,[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是()A.12B.18C.25D.90[解析]净重大于或等于78克且小于84克的频率为(0.100+0.150+0.125)×2=0.75,所以在该范围内的产品个数为120×0.75=90.[答案]D5.从甲、乙两个班各随机选出15名同学进行随堂测试(满分100分),成绩的茎叶图如图所示,则甲班学生的最高成绩为________分,乙班的及格率是________.[解析]由茎叶图可知,甲班15名同学的最高分是96,乙班同学成绩在60分及以上的共有14人,所以及格率是.[答案]966.某地政府调查了工薪阶层1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,为了了解工薪阶层对月工资收入的满意程度,要用分层抽样的方法从调查的1000人中抽出100人做电话询访,则[40,45)(百元)月工资收入段应抽出________人.[解析]月工资收入在[40,45)(百元)段的频率为1-(0.01+0.02+0.04+0.05×2)×5=0.15,则[40,45)(百元)月工资收入段的总人数为0.15×1000=150,现用分层抽样的方法从调查的1000人中抽出100人做电话询访,则[40,45)(百元)月工资收入段应抽出150×=15(人).[答案]157.将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n=________.[解析]设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,则2x+3x+4x+6x+4x+x=1,解得x=,所以前三组数据的频率分别是,,,故前三组数据的频数之和为++=27,解得n=60.[答案]608.为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示:分组(单位:岁)频数频率[20,25)50.05[25,30)①0.20[30,35)35②[35,40)300.30[40,45]100.10合计1001.00(1)频率分布表中的①②位置应填什么数据?(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数.[解](1)设年龄在[25,30)岁的频数为x,年龄在[30,35)岁的频率为y.解法一:根据题意可得=0.20,=y,解得x=20,y=0.35,故①处应填20,②处应填0.35.解法二:由题意得5+x+35+30+10=100,0.05+0.20+y+0.30+0.10=1,解得x=20,y=0.35,故①处填20,②处填0.35.(2)由频率分布表知年龄在[25,30)岁的频率是0.20,组距是5.所以==0.04.补全频率分布直方图如图所示.根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数为500×0.35=175.9.在某电脑杂志的一篇文章中,每个句子的字数如下:10,28,31,1...