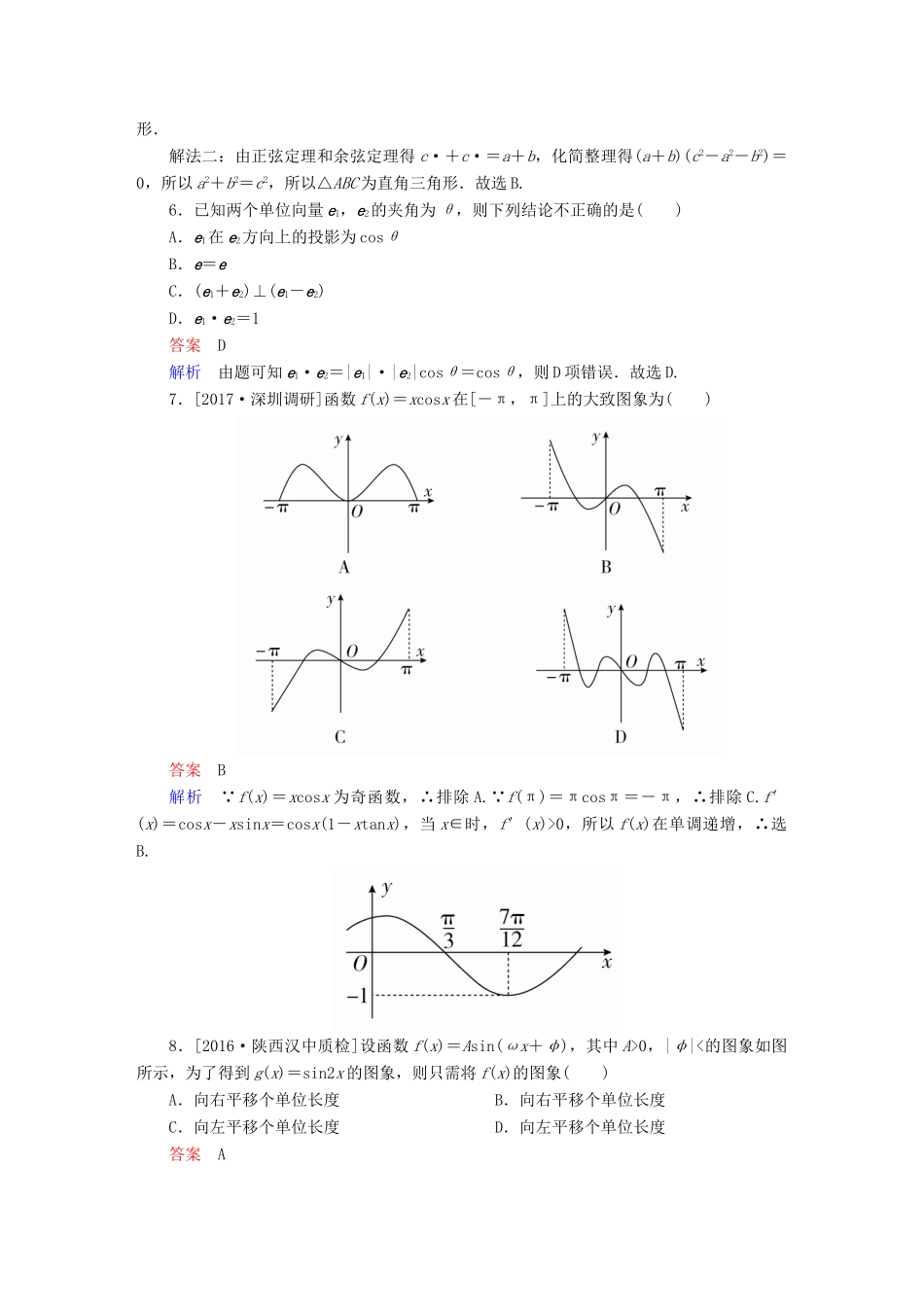
单元质量测试(三)时间:120分钟满分:150分第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.[2016·广东适应性考试]三角函数f(x)=sin-2x+cos2x的振幅和最小正周期分别是()A.,B.,πC.,D.,π答案B解析f(x)=sincos2x-cossin2x+cos2x=·cos2x-sin2x==cos2x+,所以振幅为,最小正周期T==π,故选B.2.圆弧长度等于圆内接正三角形的边长,则其圆心角弧度数为()A.B.C.D.2答案C解析设圆半径为R,则其内接正三角形的边长为R,于是圆心角的弧度数为=.3.[2016·陕西二检]若tanα=,则sin4α-cos4α的值为()A.-B.C.D.-答案D解析 tanα=,∴sin4α-cos4α=(sin2α+cos2α)·(sin2α-cos2α)==-,故选D.4.已知向量a=(1,2)与b=(4,k)垂直,且a-b与a+b的夹角为θ,则cosθ等于()A.B.C.-D.-答案D解析由a⊥b可得4+2k=0,故k=-2,∴a-b=(-3,4),a+b=(5,0),则cosθ===-.5.[2016·湖北荆门调研]在△ABC中,若sinC(cosA+cosB)=sinA+sinB,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形答案B解析解法一:sinC(cosA+cosB)=sin(π-B-C)+sin(π-A-C),sinCcosA+sinCcosB=sin(B+C)+sin(A+C),展开得sinCcosA+sinCcosB=sinBcosC+cosBsinC+sinAcosC+cosAsinC,化简整理得sinBcosC+sinAcosC=0,即(sinB+sinA)cosC=0,因为A,B是三角形的内角,所以sinA+sinB>0,所以cosC=0,即C=,故△ABC为直角三角形.解法二:由正弦定理和余弦定理得c·+c·=a+b,化简整理得(a+b)(c2-a2-b2)=0,所以a2+b2=c2,所以△ABC为直角三角形.故选B.6.已知两个单位向量e1,e2的夹角为θ,则下列结论不正确的是()A.e1在e2方向上的投影为cosθB.e=eC.(e1+e2)⊥(e1-e2)D.e1·e2=1答案D解析由题可知e1·e2=|e1|·|e2|cosθ=cosθ,则D项错误.故选D.7.[2017·深圳调研]函数f(x)=xcosx在[-π,π]上的大致图象为()答案B解析 f(x)=xcosx为奇函数,∴排除A. f(π)=πcosπ=-π,∴排除C.f′(x)=cosx-xsinx=cosx(1-xtanx),当x∈时,f′(x)>0,所以f(x)在单调递增,∴选B.8.[2016·陕西汉中质检]设函数f(x)=Asin(ωx+φ),其中A>0,|φ|<的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度答案A解析由图象可知A=1,=-=,所以T=π,又因为T=,所以ω=2,所以f(x)=sin(2x+φ),又因为f(x)的图象经过点,且|φ|<,代入解得φ=,即f(x)=sin.因为g(x)=sin2x=sin+,所以只要将f(x)=sin的图象向右平移个单位长度就可以得到g(x)的图象,故选A.9.平面向量a=(1,2),b=(4,2),c=ma+b(m∈R),且c与a的夹角等于c与b的夹角,则m=()A.-2B.-1C.1D.2答案D解析a=(1,2),b=(4,2),则c=ma+b=(m+4,2m+2),|a|=,|b|=2,∴a·c=5m+8,b·c=8m+20. c与a的夹角等于c与b的夹角,∴=,∴=,解得m=2.10.[2016·山西太原模拟]在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若sinA=,a=2,S△ABC=,则b的值为()A.B.C.2D.2答案A解析在锐角△ABC中,sinA=,S△ABC=,∴cosA==,bcsinA=bc·=,∴bc=3,①由余弦定理得a2=b2+c2-2bccosA,∴(b+c)2=a2+2bc(1+cosA)=4+6×=12,∴b+c=2.②由①②得b=c=,故选A.11.[2016·安徽十校联考]已知α为锐角,且7sinα=2cos2α,则sin=()A.B.C.D.答案A解析由7sinα=2cos2α,得7sinα=2(1-2sin2α),即4sin2α+7sinα-2=0,解得sinα=-2(舍去)或sinα=,又由α为锐角,可得cosα=,∴sin=sinα+cosα=,故选A.12.在内有两个不同的实数满足cos2x+sin2x=k+1,则实数k的取值范围是()A.0