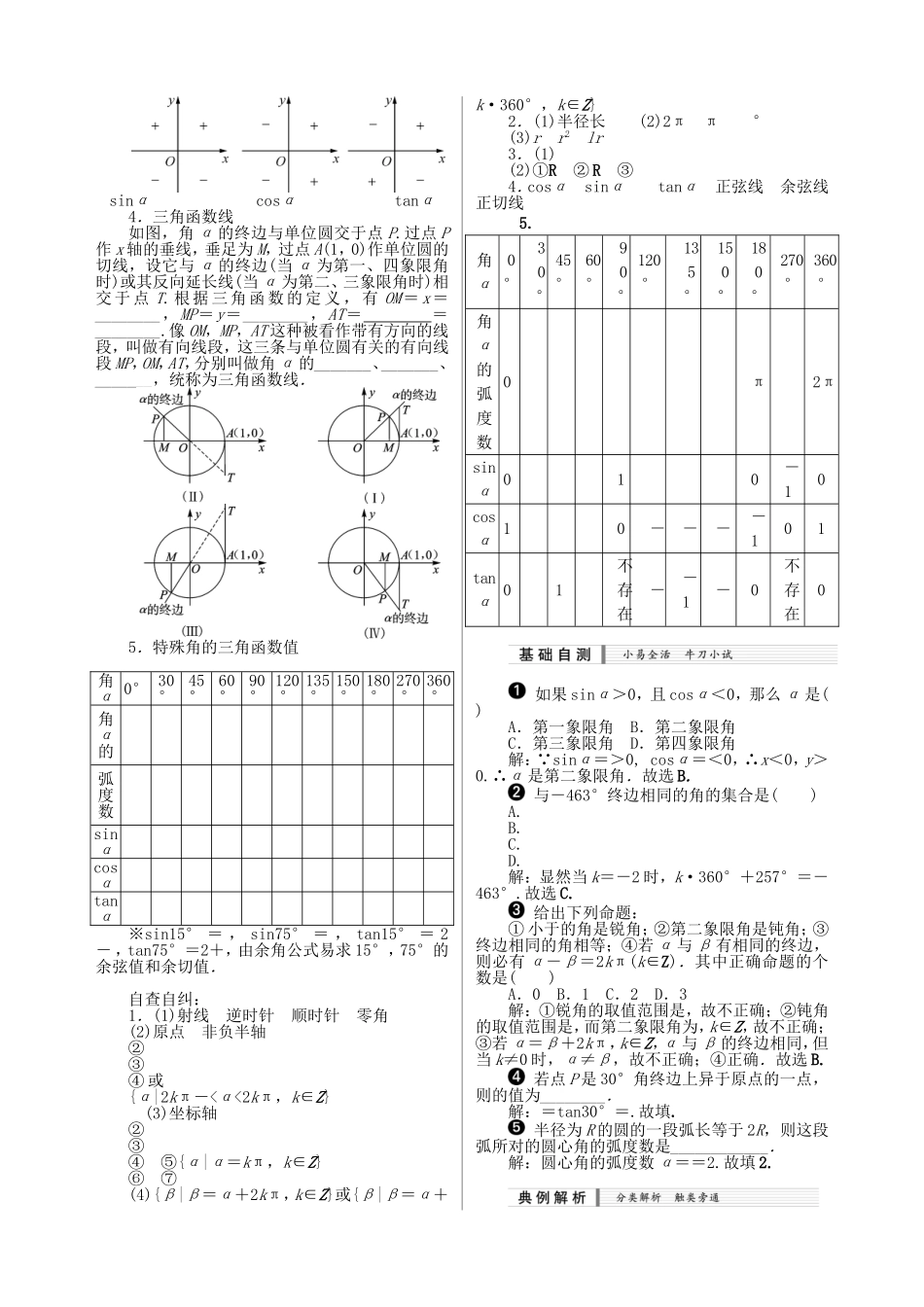
第四章三角函数(基本初等函数(Ⅱ)1.基本初等函数Ⅱ(三角函数)(1)任意角、弧度制①了解任意角的概念和弧度制的概念.②能进行弧度与角度的互化.(2)三角函数①理解任意角三角函数(正弦、余弦、正切)的定义.②能利用单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式,能画出y=sinx,y=cosx,y=tanx的图象,了解三角函数的周期性.③理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等),理解正切函数在内的单调性.④理解同角三角函数的基本关系式:sin2x+cos2x=1,=tanx.⑤了解函数y=Asin(ωx+φ)的物理意义;能画出函数y=Asin(ωx+φ)的图象,了解参数A,ω,φ对函数图象变化的影响.⑥会用三角函数解决一些简单实际问题,体会三角函数是描述周期变化现象的重要函数模型.2.三角恒等变换(1)两角和与差的三角函数公式①会用向量的数量积推导出两角差的余弦公式.②会用两角差的余弦公式推导出两角差的正弦、正切公式.③会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式,了解它们的内在联系.(2)简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但不要求记忆).3.解三角形(1)正弦定理和余弦定理掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.(2)应用能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.§4.1弧度制及任意角的三角函数1.任意角(1)角的概念角可以看成平面内一条____________绕着端点从一个位置旋转到另一个位置所成的图形.我们规定:按____________方向旋转形成的角叫做正角,按____________方向旋转形成的角叫做负角.如果一条射线没有作任何旋转,我们称它形成了一个____________.(2)象限角使角的顶点与____________重合,角的始边与x轴的____________重合.角的终边在第几象限,就说这个角是第几象限角.①α是第一象限角可表示为;②α是第二象限角可表示为;③α是第三象限角可表示为;④α是第四象限角可表示为.(3)非象限角如果角的终边在____________上,就认为这个角不属于任何一个象限.①终边在x轴非负半轴上的角的集合可记作{α|α=2kπ,k∈Z};②终边在x轴非正半轴上的角的集合可记作_______________;③终边在y轴非负半轴上的角的集合可记作________________________;④终边在y轴非正半轴上的角的集合可记作_______________________;⑤终边在x轴上的角的集合可记作_______________________;⑥终边在y轴上的角的集合可记作;⑦终边在坐标轴上的角的集合可记作.(4)终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合S=________________________.2.弧度制(1)把长度等于____________的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度.=,l是半径为r的圆的圆心角α所对弧的长.(2)弧度与角度的换算:360°=________rad,180°=________rad,1°=rad≈0.01745rad,反过来1rad=≈57.30°=57°18′.(3)若圆心角α用弧度制表示,则弧长公式l=__________;扇形面积公式S扇==.3.任意角的三角函数(1)任意角的三角函数的定义设α是一个任意角,它的终边上任意一点P(x,y)与原点的距离为r(r>0),则sinα=,cosα=,tanα=(x≠0).※cotα=(y≠0),secα=(x≠0),cscα=(y≠0).(2)正弦、余弦、正切函数的定义域三角函数定义域sinα①cosα②tanα③(3)三角函数值在各象限的符号sinαcosαtanα4.三角函数线如图,角α的终边与单位圆交于点P.过点P作x轴的垂线,垂足为M,过点A(1,0)作单位圆的切线,设它与α的终边(当α为第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于点T.根据三角函数的定义,有OM=x=________,MP=y=________,AT==________.像OM,MP,AT这种被看作带有方向的线段,叫做有向线段,这三条与单位圆有关的有向线段MP,OM,AT,分别叫做角α的_______、_______、_______,统称为三角函数线.5.特殊角的三角函数值角α0°30°45°60°90°120°135°150°180°270...