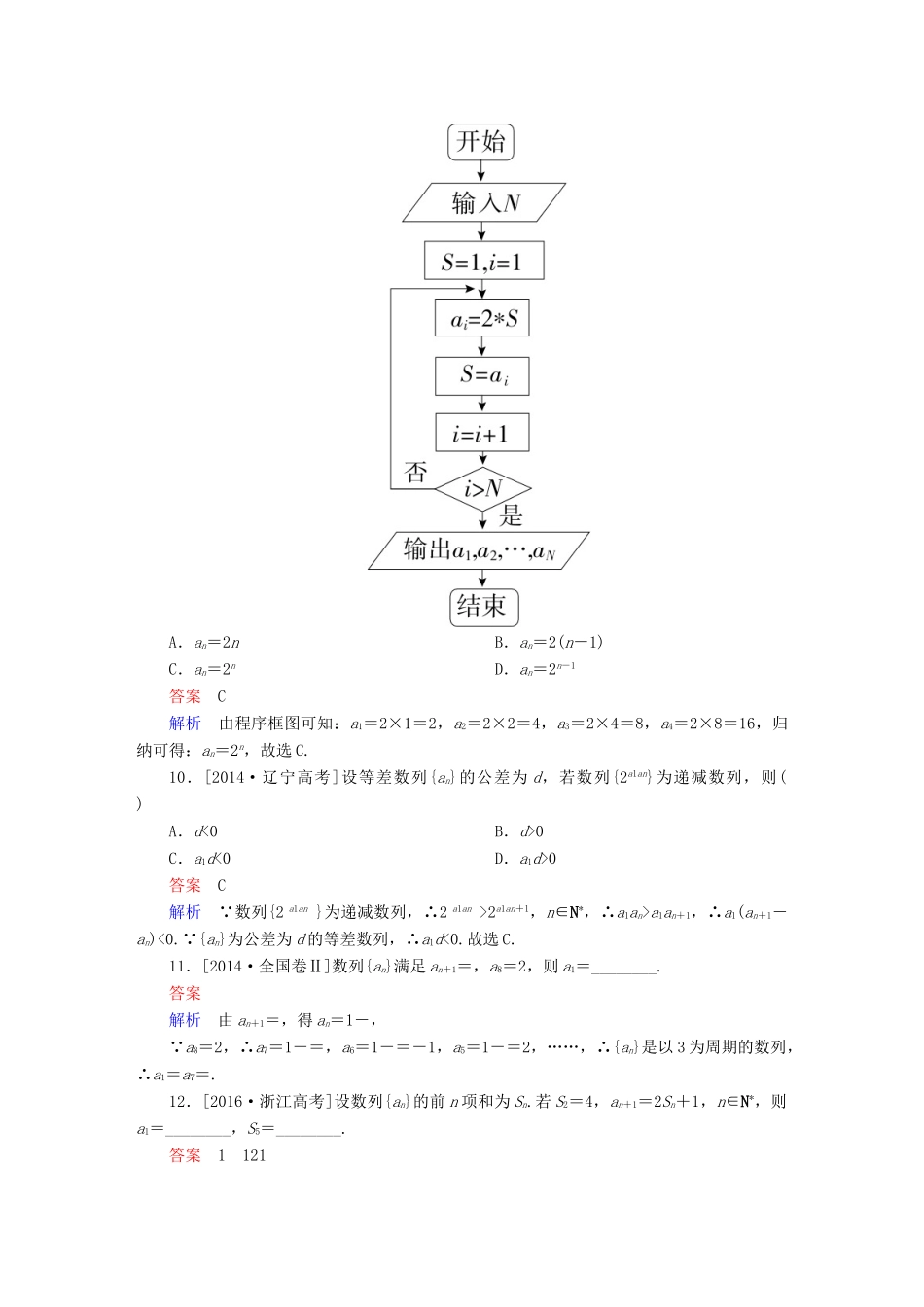
考点测试29数列的概念与简单表示法一、基础小题1.已知数列{an}的通项公式an=(n∈N*),则是这个数列的()A.第8项B.第9项C.第10项D.第12项答案C解析由题意知=,n∈N*,解得n=10,即是这个数列的第10项,故选C.2.已知数列{an}的前n项和为Sn,且Sn=2(an-1),则a2等于()A.4B.2C.1D.-2答案A解析由Sn=2(an-1),得a1=2(a1-1),即a1=2,又a1+a2=2(a2-1),得a2=4.3.已知数列{an}满足a1=0,an+1=an+2n-1,则数列{an}的一个通项公式为()A.an=n-1B.an=(n-1)2C.an=(n-1)3D.an=(n-1)4答案B解析a1=0,an+1=an+2n-1,所以a2=0+1=1,a3=1+3=4,a4=4+5=9,故数列{an}的一个通项公式为an=(n-1)2.4.设an=-2n2+29n+3,则数列{an}的最大项是()A.107B.108C.D.109答案B解析因为an=-2n2+29n+3=-22+,n∈N*,所以当n=7时,an取得最大值108.5.数列{an}中,a1=1,对于所有的n≥2,n∈N都有a1·a2·a3·…·an=n2,则a3+a5=()A.B.C.D.答案A解析解法一:令n=2,3,4,5,分别求出a3=,a5=,∴a3+a5=,故选A.解法二:当n≥2时,a1·a2·a3·…·an=n2.当n≥3时,a1·a2·a3·…·an-1=(n-1)2.两式相除得an=2,∴a3=,a5=,∴a3+a5=,故选A.6.已知在数列{an}中,a1=2,a2=7,若an+2等于anan+1(n∈N*)的个位数,则a2016的值为()A.8B.6C.4D.2答案B解析因为a1a2=2×7=14,所以a3=4;因为a2a3=7×4=28,所以a4=8;因为a3a4=4×8=32,所以a5=2;因为a4a5=8×2=16,所以a6=6;因为a5a6=2×6=12,所以a7=2;因为a6a7=6×2=12,所以a8=2;依次计算得a9=4,a10=8,a11=2,a12=6,所以从第3项起,数列{an}成周期数列,周期为6,因为2016=2+335×6+4,所以a2016=6.7.已知Sn是数列{an}的前n项和,且有Sn=n2+1,则数列{an}的通项an=________.答案解析当n=1时,a1=S1=1+1=2,当n≥2时,an=Sn-Sn-1=(n2+1)-[(n-1)2+1]=2n-1.此时对于n=1不成立,故an=8.数列{an}满足a1+a2+…+an=3n+1,n∈N*,则an=________.答案解析当n=1时,a1=12.因为a1+a2+…+an=3n+1,n∈N*,①所以当n≥2时,a1+a2+…+an-1=3n-2.②所以①-②,得an=3n+1.所以an=二、高考小题9.[2014·陕西高考]根据下面框图,对大于2的整数N,输出的数列的通项公式是()A.an=2nB.an=2(n-1)C.an=2nD.an=2n-1答案C解析由程序框图可知:a1=2×1=2,a2=2×2=4,a3=2×4=8,a4=2×8=16,归纳可得:an=2n,故选C.10.[2014·辽宁高考]设等差数列{an}的公差为d,若数列{2a1an}为递减数列,则()A.d<0B.d>0C.a1d<0D.a1d>0答案C解析 数列{2a1an}为递减数列,∴2a1an>2a1an+1,n∈N*,∴a1an>a1an+1,∴a1(an+1-an)<0. {an}为公差为d的等差数列,∴a1d<0.故选C.11.[2014·全国卷Ⅱ]数列{an}满足an+1=,a8=2,则a1=________.答案解析由an+1=,得an=1-, a8=2,∴a7=1-=,a6=1-=-1,a5=1-=2,……,∴{an}是以3为周期的数列,∴a1=a7=.12.[2016·浙江高考]设数列{an}的前n项和为Sn.若S2=4,an+1=2Sn+1,n∈N*,则a1=________,S5=________.答案1121解析解法一: an+1=2Sn+1,∴a2=2S1+1,即S2-a1=2a1+1,又 S2=4,∴4-a1=2a1+1,解得a1=1.又an+1=Sn+1-Sn,∴Sn+1-Sn=2Sn+1,即Sn+1=3Sn+1,由S2=4,可求出S3=13,S4=40,S5=121.解法二:由an+1=2Sn+1,得a2=2S1+1,即S2-a1=2a1+1,又S2=4,∴4-a1=2a1+1,解得a1=1.又an+1=Sn+1-Sn,∴Sn+1-Sn=2Sn+1,即Sn+1=3Sn+1,则Sn+1+=3,又S1+=,∴是首项为,公比为3的等比数列,∴Sn+=×3n-1,即Sn=,∴S5==121.13.[2015·江苏高考]设数列{an}满足a1=1,且an+1-an=n+1(n∈N*),则数列前10项的和为________.答案解析由已知得,a2-a1=1+1,a3-a2=2+1,a4-a3=3+1,…,an-an-1=n-1+1(n≥2),则有an-a1=1+2+3+…+n-1+(n-1)(n≥2),因为a1=1,所以an=1+2+3+…+n(n≥2),即an=(n≥2),又当n=1时,a1=1也...