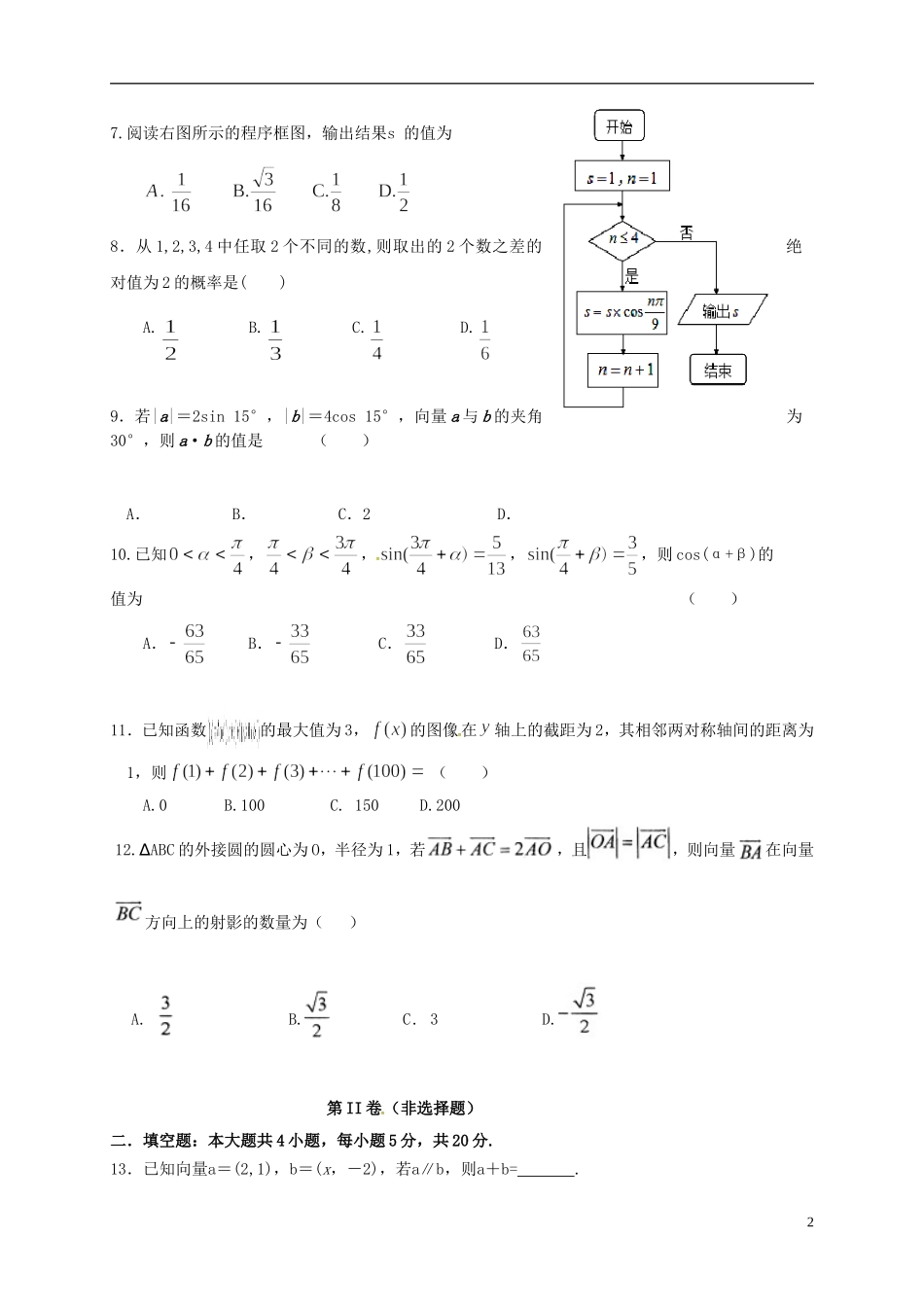
抚顺市2016-2017下学期高一期末考试数学试卷本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间为120分钟。第I卷(60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。1.的值是()A.B.C.D.2.一段圆弧的长度等于其圆内接正三角形的边长,则其圆心角的弧度数为()A.B.C.D.3.2014年3月,为了调查教师对第十二届全国人民代表大会第二次会议的了解程度,抚顺市拟采用分层抽样的方法从三所不同的中学抽取60名教师进行调查。已知学校中分别有180、270、90名教师,则从学校中应抽取的人数为()A.10B.12C.18D.244.已知变量与正相关,且由观测数据算得样本平均数,则由该观测的数据算得的线性回归方程可能是()A.B.C.D.5.某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则的值为()A.9B.10C.11D.136.某学校为了解高一年级l203名学生对某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为()A.40B.30.1C.30D.1217.阅读右图所示的程序框图,输出结果s的值为8.从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是()A.B.C.D.9.若|a|=2sin15°,|b|=4cos15°,向量a与b的夹角为30°,则a·b的值是()A.B.C.2D.10.已知,,,,则cos(α+β)的值为()A.B.C.D.11.已知函数的最大值为3,的图像在轴上的截距为2,其相邻两对称轴间的距离为1,则()A.0B.100C.150D.20012.∆ABC的外接圆的圆心为O,半径为1,若,且,则向量在向量方向上的射影的数量为()A.B.C.3D.第II卷(非选择题)二.填空题:本大题共4小题,每小题5分,共20分.13.已知向量a=(2,1),b=(x,-2),若a∥b,则a+b=.214.用秦九韶算法计算f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值时,的值为_____.15.在边长为2的正三角形ABC内任取一点P,则使点P到三个顶点的距离至少有一个小于1的概率是________.16.三角形ABC是锐角三角形,若角θ终边上一点P的坐标为(sinA-cosB,cosA-sinB),则++的值是.三.解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知角为第三象限角,,若,求的值.18.(本小题满分12分)我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准0〜3.5,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了100位居民某年的月均用水量(单位:t),制作了频率分布直方图.(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准0〜3.5,则月均用水量的最低标准定为多少吨,请说明理由;(3)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).319.(本小题满分12分)已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点.(1)求圆的方程;(2)当时,求直线的方程.20.(本小题满分12分)一个包装箱内有6件产品,其中4件正品,2件次品。现随机抽出两件产品,(1)求恰好有一件次品的概率。(2)求都是正品的概率。21.(本小题满分12分)已知向量,记函数.求:(I)函数的最小值及取得最小值时的集合;(II)函数的单调递增区间.22.(本小题满分12分)已知函数.(1)若对任意的,均有,求的取值范围;(2)若对任意的,均有,求的取值范围.4抚顺市2016-2017下学期高一期末考试数学答案一.选择题1.C2.C3.A4.B5.D6.C7.A8.B9.B10.B11.D12.A二.填空题13.(-2,-1)14.8015.16.-1三.解答题18.5...........5分..........7分.........10分19.(1);(2)或.试题解析:(1)由题意知到直线的距离为圆半径圆的方程为[.......5分(2)设线段的中点为,连结,则由垂径定理可知,且,在中由勾股定理易知...