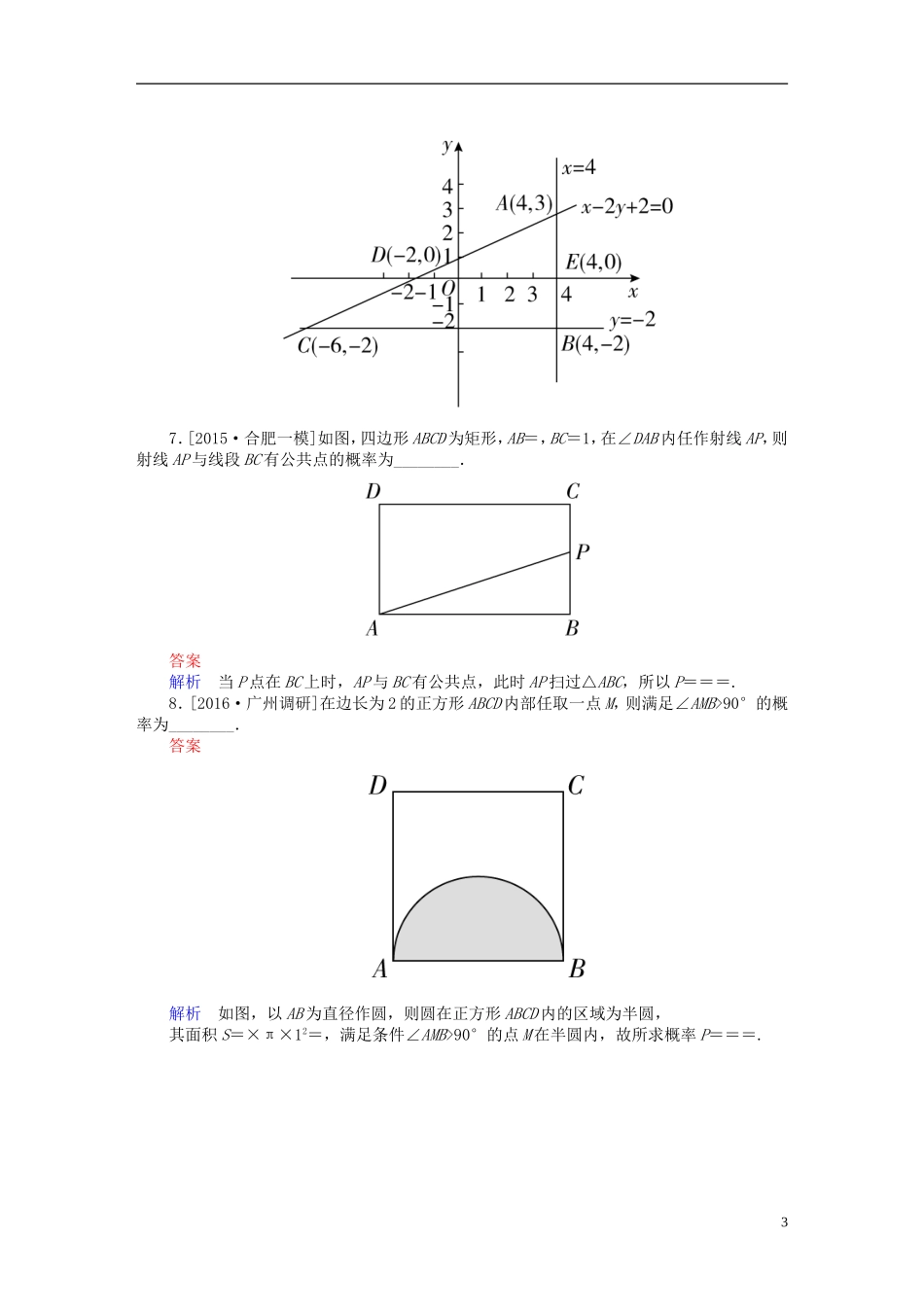
10-3几何概型练习文[A组·基础达标练]1.在长为12cm的线段AB上任取一点M,并以线段AM为边作正方形,则此正方形的面积介于36cm2与81cm2之间的概率为()A.B.C.D.答案A解析由题意可知,6≤AM≤9,于是所求的概率为P==.2.[2016·河南三市联考]在区间[-π,π]内随机取两个数分别为a,b,则使得函数f(x)=x2+2ax-b2+π2有零点的概率为()A.1-B.1-C.1-D.1-答案B解析函数f(x)=x2+2ax-b2+π2有零点,需Δ=4a2-4(-b2+π2)≥0,即a2+b2≥π2成立.而a,b∈[-π,π],建立平面直角坐标系,满足a2+b2≥π2的点(a,b)如图阴影部分所示,所求事件的概率为P===1-.3.在棱长为3的正方体ABCD-A1B1C1D1内任取一点P,则点P到正方体各面的距离都不小于1的概率为()A.B.C.D.答案A解析正方体中到各面的距离不小于1的点的集合是一个中心与原正方体中心重合,且棱长为1的正方体,该正方体的体积是V1=13=1,而原正方体的体积为V=33=27,故所求的概率为P==.4.[2014·湖北高考]由不等式组确定的平面区域记为Ω1,不等式组确定的平面区域记为Ω2.在Ω1中随机取一点,则该点恰好在Ω2内的概率为()A.B.C.D.答案D1解析由题意作图,如图所示,Ω1的面积为×2×2=2,图中阴影部分的面积为2-××=,则所求概率P==.5.[2015·陕西高考]设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为()A.+B.+C.-D.-答案C解析 |z|=≤1,∴(x-1)2+y2≤1,其几何意义表示为以(1,0)为圆心,1为半径的圆面,如图所示,而y≥x所表示的区域如图中阴影部分,故P==-.6.[2016·昌平模拟]设不等式组表示的平面区域为D.在区域D内随机取一个点,则此点到直线y+2=0的距离不小于2的概率是()A.B.C.D.答案D解析作出平面区域D,可知平面区域D是以A(4,3),B(4,-2),C(-6,-2)为顶点的三角形区域,当点在△AED区域内时,点到直线y+2=0的距离不小于2.∴P===.27.[2015·合肥一模]如图,四边形ABCD为矩形,AB=,BC=1,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为________.答案解析当P点在BC上时,AP与BC有公共点,此时AP扫过△ABC,所以P===.8.[2016·广州调研]在边长为2的正方形ABCD内部任取一点M,则满足∠AMB>90°的概率为________.答案解析如图,以AB为直径作圆,则圆在正方形ABCD内的区域为半圆,其面积S=×π×12=,满足条件∠AMB>90°的点M在半圆内,故所求概率P===.39.[2015·福建高考]如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且点C与点D在函数f(x)=的图象上.若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于________.答案解析依题意得,点C的坐标为(1,2),所以点D的坐标为(-2,2),所以矩形ABCD的面积S矩形ABCD=3×2=6,阴影部分的面积S阴影=×3×1=,根据几何概型的概率求解公式,得所求的概率P===.10.[2016·浙江联考]一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.答案解析列举可知,共有36种情况.和为4的情况有10种,所以所求的概率为P==.[B组·能力提升练]1.[2015·湖北高考]在区间[0,1]上随机取两个数x,y,记p1为事件“x+y≥”的概率,p2为事件“|x-y|≤”的概率,p3为事件“xy≤”的概率,则()A.p1