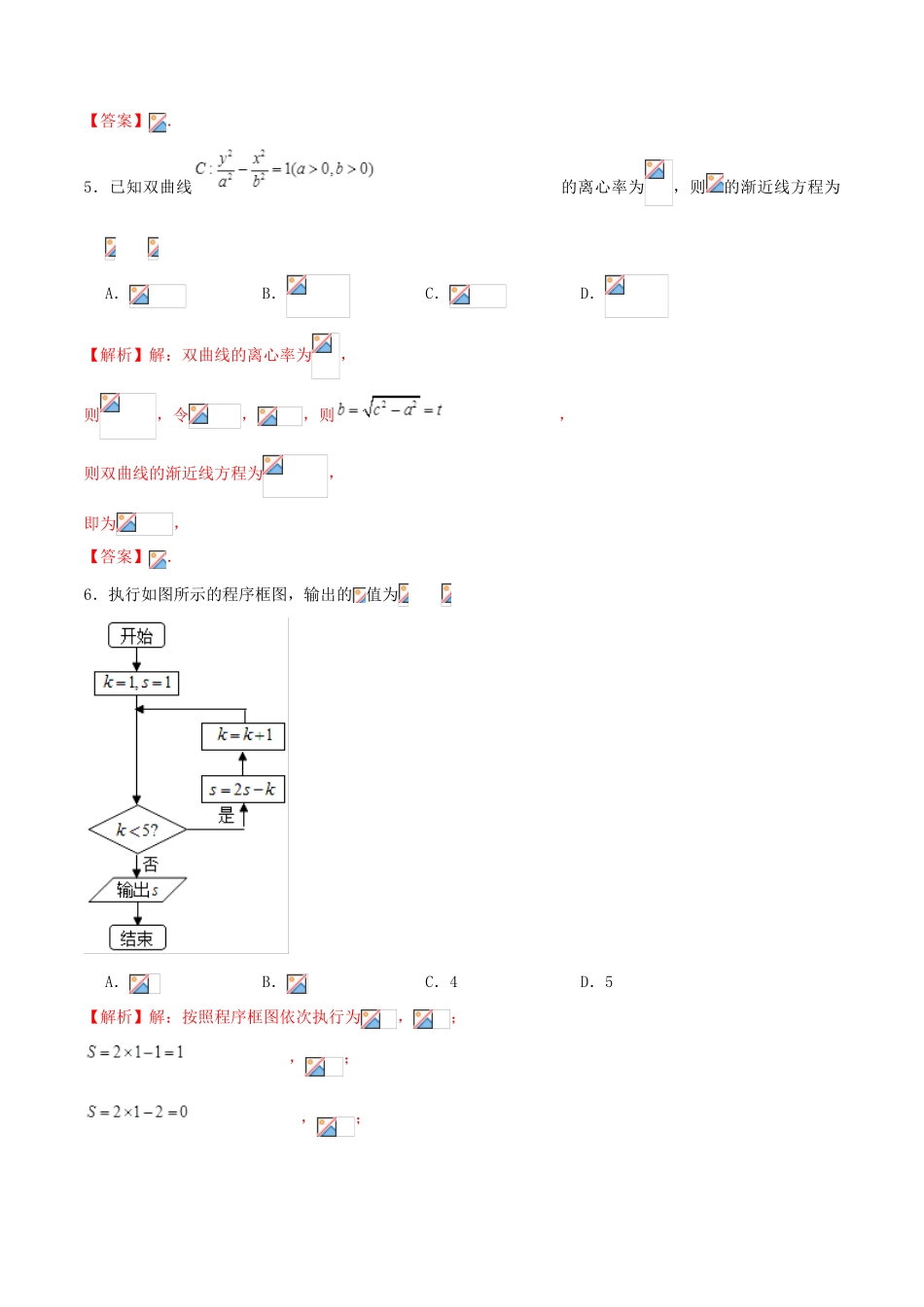
专题14高考数学仿真押题试卷(十四)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。4.考试结束后,请将本试题卷和答题卡一并上交。第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,,则等于A.,B.C.,D.【解析】解:由,又,全集,所以.所以,.【答案】.2.已知复数,则A.B.C.D.【解析】解:,则,【答案】.3.设是公差为的等差数列,是前项的和,若,,成等比数列,则A.2B.C.D.【解析】解:是公差为的等差数列,是前项的和,,,成等比数列,,即,解得.【答案】.4.若变量,满足约束条件,则的最大值是A.2B.4C.7D.8【解析】解:满足约束条件的可行域如下图中阴影部分所示:目标函数,,,,,故的最大值是7,【答案】.5.已知双曲线的离心率为,则的渐近线方程为A.B.C.D.【解析】解:双曲线的离心率为,则,令,,则,则双曲线的渐近线方程为,即为,【答案】.6.执行如图所示的程序框图,输出的值为A.B.C.4D.5【解析】解:按照程序框图依次执行为,;,;,;,;,,退出循环,输出.【答案】.7.已知函数,则定积分的值为A.B.C.D.【解析】解:,其中,其中表示以为圆心,以1为半径的圆的面积的二分之一,故,故,【答案】.8.函数某相邻两支图象与坐标轴分别变于点,则方程所有解的和为A.B.C.D.【解析】解:相邻两支图象与坐标轴分别变于点,函数的周期,则,此时,又,得,即,,当时,,则,与的对称中心相同,与的交点关于同一个对称中心对称,由,,得,,,,当时,,即两个好的对称中心为,,由图象知两个函数只有两个交点,则,,【答案】.9.已知某长方体的三视图如图所示,在该长方体的一组相对侧面,上取三点,,,其中为侧面的对角线上一点(与对角线端点小重合),,为侧面的一条对角线的两个端点.若以线段为直径的圆过点,则的最小值为A.B.C.4D.2【解析】解:根据长方体的三视图知,该长方体的底面是边长为2的正方形,且高为,如图所示;由题意知,为圆的直径,则的最小值为,此时为直角三角形,的最小值为.【答案】.10.已知双曲线的左、右焦点分别为,,抛物线与双曲线交于纵坐标为1的点,直线与抛物线的准线交于,若,则双曲线的方程为A.B.C.D.【解析】解:抛物线与双曲线交于纵坐标为1的点,可得,,抛物线的准线方程为,的横坐标为,设,由,可得,解得,可得焦点为,,由双曲线的定义可得,可得,,则双曲线的方程为.【答案】.11.某观察者站在点观察练车场上匀速行驶的小车的运动情况,小车从点出发的运动轨迹如图所示.设观察者从点开始随动点变化的视角为,练车时间为,则函数的图象大致为A.B.C.D.【解析】解:根据小车从点出发的运动轨迹可得,视角的值先是匀速增大,然后又减小,接着基本保持不变,然后又减小,最后又快速增大,【答案】.12.定义,已知,为函数的两个零点,若存在整数满足,则,的值A.一定大于B.一定小于C.一定等于D.一定小于【解析】解:由题意可知,,,由根与系数的关系可得:,,当时,有,即,所以,所以,因为,则,的值一定小于,【答案】.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.某人在公园进行射击气球游戏,排除其它因素的影响,各次射击相互独立,每次击中气球的概率均为0.8,若连续射击10次,记击中气球的次数为,则1.6.【解析】解:由题意可知各次射击相互独立,每次击中气球的概率均为0.8,若连续射击10次,记击中气球的次数为,可得,所以.故答案为:1.6.14.若实数,满足约束条件,则的最大值是9.【解析】解:作出实数,满足约束条件对应的平面区域如图:由得,平移直线,由图象可知当直线,经过点时,直线,的截距最小,此时最大,由...