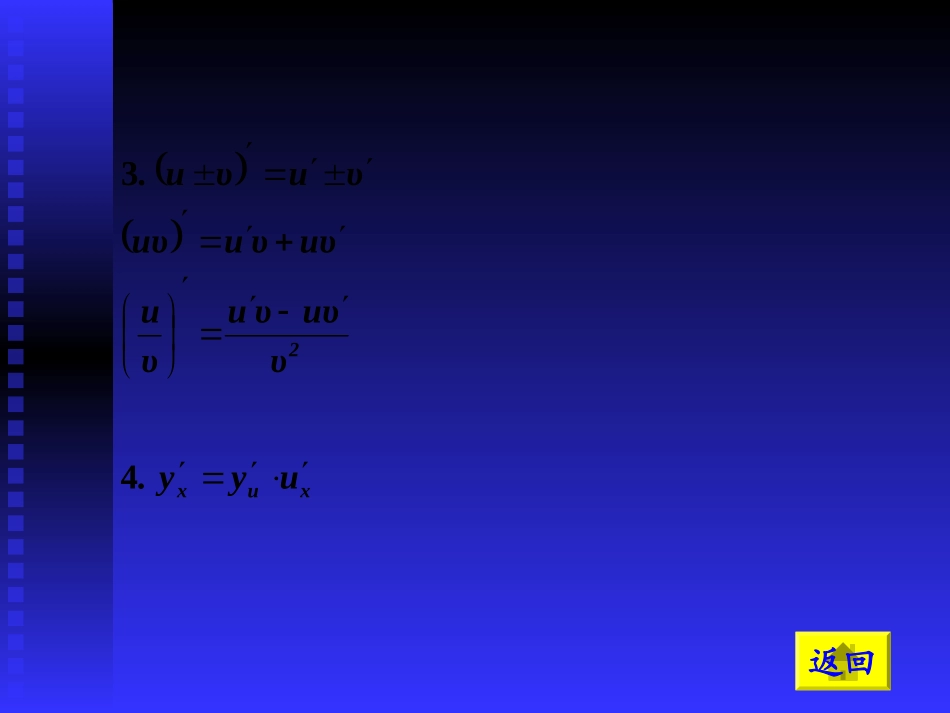高中数学基础复习 第十二章 极限与导数 第2课时 导数VIP免费

要点·疑点·考点要点·疑点·考点课前热身课前热身能力·思维·方法能力·思维·方法延伸·拓展延伸·拓展误解分析误解分析第2课时导数要点要点··疑点疑点··考点考点xxfxxfxyxf.xx00limlim1xx-mmeexxxxmmxxCC.sincoscossinQ021为常数exxxxaaaaaxxlog1log1lnln返回2υυuυuυuυuυuuυυuυu.3xuxuyy.4课前热身1.已知y=x3-2x+1，则y′=3x2-2，y′|x=_______.10B2.曲线y=2x-x3在横坐标为-1的点处的切线为l，则点(3，2)到l的距离等于()A.B.C.D.227221110109229A3.若f′(x0)=2，则等于()(A)-1(B)-2(C)1(D)1/2kxfkxfk2lim000B4.函数y=xcosx-sinx的导数为()(A)xsinx(B)-xsinx(C)xcosx(D)-xcosx返回5.函数y=xe1-cosx的导数为()(A)(1+xsinx)e1+cosx(B)(1+xsinx)e1-cosx(C)(1-xsinx)e1+cosx(D)(1-xsinx)e1-cosxA能力能力··思维思维··方法方法1.已知抛物线y=x2-4与直线y=x+2.求(1)两曲线的交点；(2)抛物线在交点处的切线方程.【解题回顾】同样的方法用于其他的问题背景可能是求运动的瞬时速度及边际成本等2.确定抛物线方程y=x2+bx+c中的常数b和c，使得抛物线和直线y=2x在x=2处相切【解题回顾】待定系数法是数学中的一个重要思想方法，应掌握3.(1)求函数f(x)=3x2在x=1处的导数；(2)求y=2xx的导数xxy2【解题回顾】幂指函数的求导，常用取对数法解之.返回4.已知y=sinx的导函数为y′=cosx求证：sinx＜x(0＜x＜π/2)【解题回顾】本题如用单位圆中正弦线与弧长之长比较，答案很明显,但有失严密，所以证明题一般不用数形结合法.延伸延伸··拓展拓展【解题回顾】要善于分析复杂函数的结构特点，合理将之分解成简单函数的复合。返回5.求函数的导数21logx-ya误解分析误解分析本节里容易出错的地方就是复合函数求导，要正确分离中间变量，严格按复合函数求导法则操作，可以避免错误返回