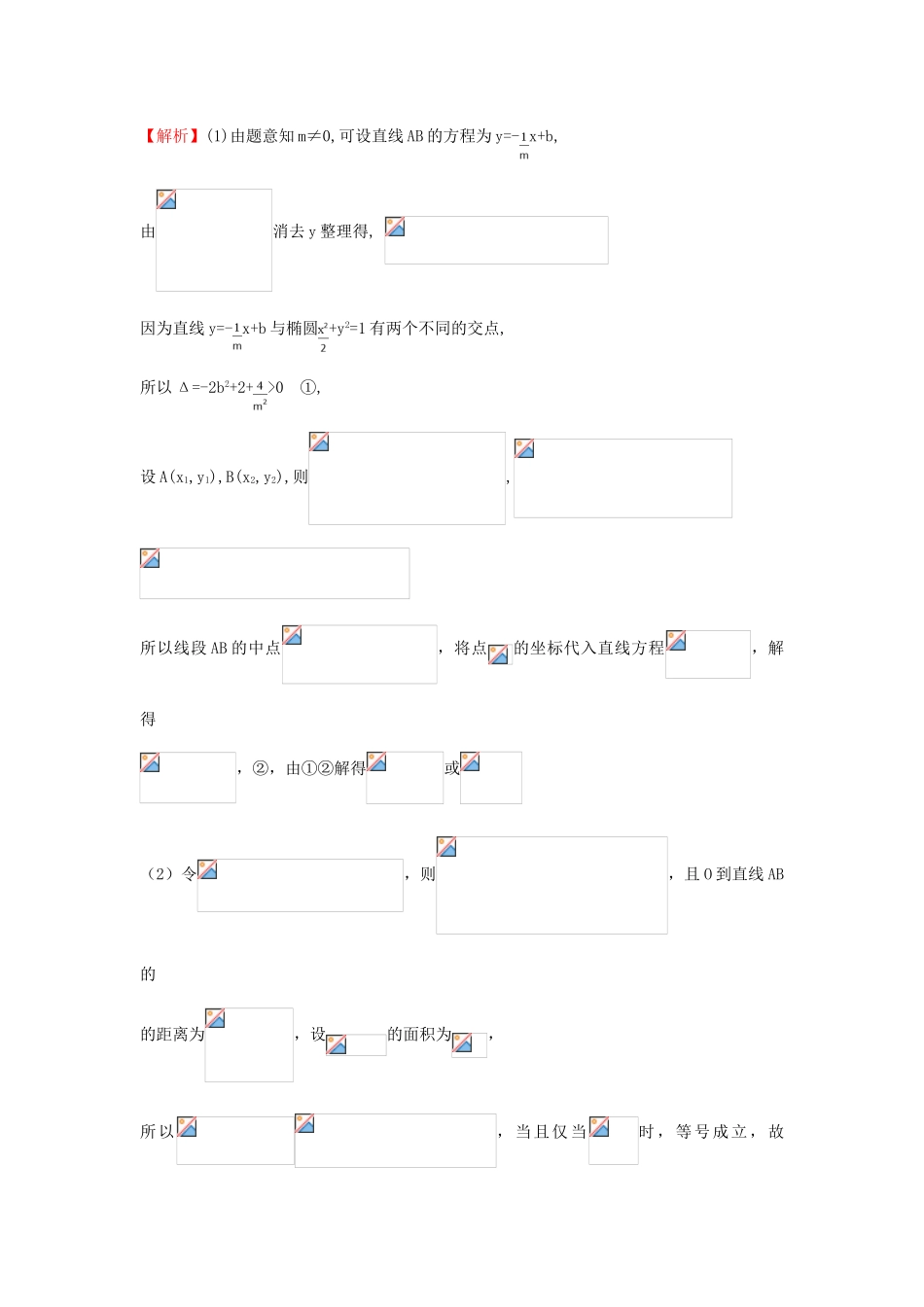
考点36椭圆一、选择题1.(2015·广东高考文科·T8)已知椭圆+=1(m>0)的左焦点为F1(-4,0),则m=()A.9B.4C.3D.2【解题指南】本题考查了椭圆的几何性质,根据焦点在x轴上,判断出m2<25,进而根据焦点坐标,a2的值及m>0求得m.【解析】选C.由题意得:m2=25-42=9,因为m>0,所以m=3.2.(2015·福建高考文科·T11)已知椭圆E:+=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点.若|AF|+|BF|=4,点M到直线l的距离不小于,则椭圆E的离心率的取值范围是()A.B.C.D.【解题指南】利用椭圆的定义求出a,点M到直线l的距离不小于求出b的范围,从而求出离心率的范围.【解析】选A.不妨设左焦点为F2,连接AF2,BF2,由椭圆的对称性可知四边形AFBF2的对角线互相平分,所以四边形AFBF2为平行四边形,所以+=+=2a=4,所以a=2,设M(0,b),所以所以,又,所以.二、填空题3.(2015·浙江高考文科·T15)椭圆()的右焦点关于直线的对称点在椭圆上,则椭圆的离心率是.【解题指南】利用已知条件求出点Q的坐标,从而求出a,b,c的关系.【解析】设F(c,0)关于直线y=x的对称点为Q(m,n),则有,解得,所以在椭圆上,即有,解得,所以离心率答案:三、解答题4.(2015·浙江高考理科·T19)已知椭圆+y2=1上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围.(2)求△AOB面积的最大值(O为坐标原点).【解题指南】(1)可设直线AB的方程为y=-x+b,从而可知有两个不同的解,再由AB中点也在直线上,即可得到关于m的不等式,从而求解.(2)令t=,可将△AOB表示为t的函数,从而将问题等价转化为在给定范围上求函数的最值,从而求解.【解析】(1)由题意知m≠0,可设直线AB的方程为y=-x+b,由消去y整理得,因为直线y=-x+b与椭圆+y2=1有两个不同的交点,所以Δ=-2b2+2+>0①,设A(x1,y1),B(x2,y2),则,所以线段AB的中点,将点的坐标代入直线方程,解得,②,由①②解得或(2)令,则,且O到直线AB的的距离为,设的面积为,所以,当且仅当时,等号成立,故面积的最大值为.5.(2015·新课标全国卷Ⅱ文科·T20)已知椭圆C:(a>b>0)的离心率为,点(2,)在C上.(1)求C的方程.(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.【解析】(1)由题意有,,解得,所以C的方程为.(2)设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM).将y=kx+b代入得.,.于是直线的斜率,即所以直线OM的斜率与直线l的斜率的乘积为定值.6.(2015·陕西高考理科·T20)已知椭圆Ε:+=1(a>b>0)的半焦距为c,原点Ο到经过两点(c,0),(0,b)的直线的距离为c.(1)求椭圆Ε的离心率;(2)如图,ΑΒ是圆Μ:(x+2)2+(y-1)2=的一条直径,若椭圆Ε经过Α,Β两点,求椭圆Ε的方程.【解题指南】(1)求出经过点(0,b)和(c,0)的直线方程,运用点到直线的距离公式,结合离心率公式计算即可得到所求值.(2)由(1)知,椭圆E的方程为x2+4y2=4b2,①设出直线AB的方程,代入椭圆方程,运用根与系数的关系和弦长公式,结合圆的直径和中点坐标公式,解方程可得b2=3,即可得到椭圆方程.【解析】(1)过点(c,0),(0,b)的直线方程为bx+cy-bc=0,则原点O到直线的距离,由,得,解得离心率.(2)由(1)知,椭圆E的方程为x2+4y2=4b2.①依题意,圆心M(-2,1)是线段AB的中点,且|AB|=.易知,AB不与x轴垂直,设其直线方程为y=k(x+2)+1,代入①得(1+4k2)x2+8k(2k+1)x+4(2k+1)2-4b2=0,设A(x1,y1),B(x2,y2),则由,得解得.从而.于是.由,得,解得.故椭圆E的方程为.7.(2015·陕西高考文科·T20)(本小题满分12分)如图,椭圆E:+=1(a>b>0)经过点A(0,-1),且离心率为.(1)求椭圆E的方程.(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.【解题指南】(1)先由已知求出椭圆长半轴长,进而得出椭圆的标准方程.(2)将直线方程代入椭圆方程,得两根之和与两根之积与k的关系式,将之代入直线AP与AQ的斜率之和整理式消k后得证.【解析】(1)由题意知=,b=1,综合a2=b2+c2,解得a=,所以,椭圆的方程为+y2=1.(2)由题设知,直线PQ的方程为y=k(x-1)+1,代入+y2=1,得(1+2k2)x2-4k(k-1)x+2k(k-2)=0,由已知Δ>0,设P(x1,y1),Q(x2,y2),x1x2≠0,则,从而直线与的斜率之和.