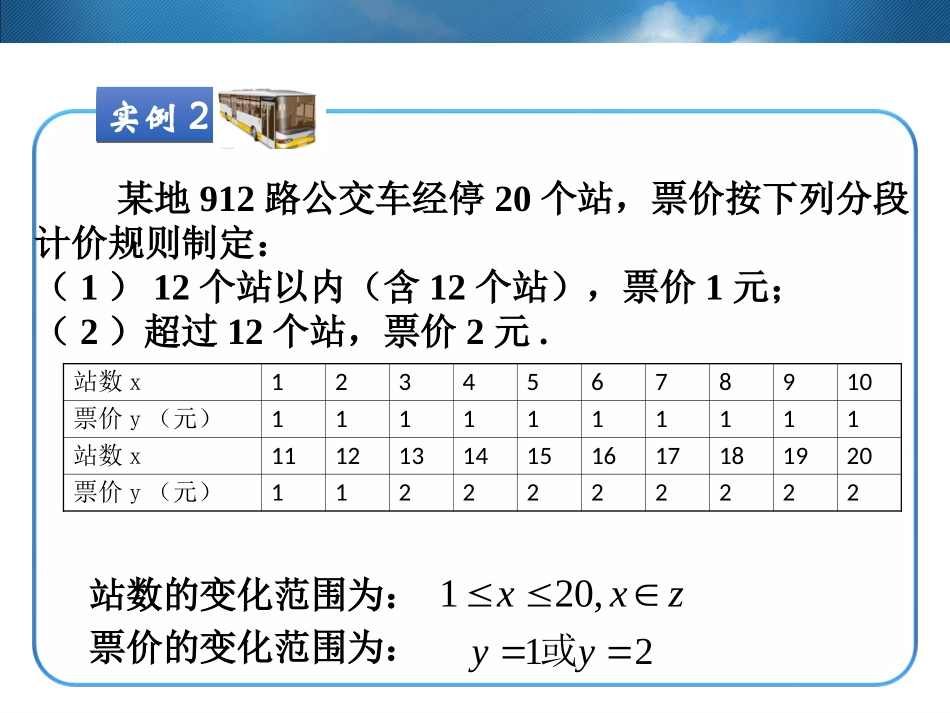
函数的概念实例1实例1气温的变化范围为:3040t平均鸣叫次数的范围为:189259k某地有一种蟋蟀,当气温t在30ºC至40ºC之间变化时,它在一分钟里平均鸣叫的次数与气温有关,k表示对应的平均鸣叫次数,他们的关系可以近似地用一次函数表示成.(*)721kt实例2实例2某地912路公交车经停20个站,票价按下列分段计价规则制定:(1)12个站以内(含12个站),票价1元;(2)超过12个站,票价2元.站数x12345678910票价y(元)1111111111站数x11121314151617181920票价y(元)1122222222票价的变化范围为:12yy或站数的变化范围为:120,xxz实例1实例1气温的变化范围为:3040t平均鸣叫次数的范围为:189259k某地有一种蟋蟀,当气温t在30ºC至40ºC之间变化时,它在一分钟里平均鸣叫的次数与气温有关,k表示对应的平均鸣叫次数,他们的关系可以近似地用一次函数表示成.(*)721kt实例2实例2某地912路公交车经停20个站,票价按下列分段计价规则制定:(1)12个站以内(含12个站),票价1元;(2)超过12个站,票价2元.站数x12345678910票价y(元)1111111111站数x11121314151617181920票价y(元)1122222222票价的变化范围为:12yy或站数的变化范围为:120,xxz实例2实例2实例1实例1(1)A,B为非空数集;(2)对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应.共同特征气温的变化范围为集合:{|3040}Att平均鸣叫的次数范围为集合:{|189259}Bkk公交车站数的变化范围为集合:{|120,}Axxxz票价的变化范围为集合:{1,2}B实例3实例3近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.图1中的曲线显示了南极上空臭氧层空洞的面积S(单位:106km2)随时间t(单位:年)从1979~2001年的变化情况.实例3实例3时间t的变化范围为数集:A={t|1979≤t≤2001}臭氧层空洞面积S的变化范围为数集:B={S|0≤S≤26}对于数集A中的任意一个t在数集B中都有唯一确定的S和它对应你能写出臭氧层空洞面积S与时间t的函数表达式吗?没有表达式的情况下,臭氧层空洞面积S与时间t是通过什么方式对应的呢?实例3实例3近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.图1中的曲线显示了南极上空臭氧层空洞的面积S(单位:106km2)随时间t(单位:年)从1979~2001年的变化情况.实例1实例1某地有一种蟋蟀,当气温t在30ºC至40ºC之间变化时,它在一分钟里平均鸣叫的次数与气温有关,k表示对应的平均鸣叫次数,他们的关系可以近似地用一次函数表示成.(*)721kt实例2实例2某地912路公交车经停20个站,票价按下列分段计价规则制定:(1)12个站以内(含12个站),票价1元;(2)超过12个站,票价2元.站数x12345678910票价y(元)1111111111站数x11121314151617181920票价y(元)1122222222共同特征(1)A,B为非空数集;(2)按照某种确定的对应关系;(3)对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应.三个实例中的函数关系可以描述为:三个实例中的函数关系可以描述为:函数概念定义域,值域,对应关系函数三要素:函数三要素:1.函数的概念3.函数的三要素定义域,值域,对应关系2.函数符号1.课后练习完成下列表格2.阅读提升结合教材26页函数概念的发展历史,阅读下发的资料;并自己动手查阅各种资料多方面了解函数概念的发展历史.